학습 길잡이 기타
-
학습 길잡이 기타
싸움을 잘하는 사람은 적을 끌어들이지 적에게 끌려 다니지 않는다 - 손자
『손자병법』의 ‘허실’편에 실려 있는 글로, “무릇 싸움터에 먼저 도착하여 적을 기다리면 편안하고, 싸움터에 늦게 도착해 허겁지겁 싸우면 피곤하다. 싸움을 잘하는 사람은 적을 끌어들이지 적에게 끌려 다니지 않는다.”의 일부예요.상대가 주도권을 쥐고 있을 때, 쫓기듯이 일처리를 하면 실수가 많아져요. 그리고 조급하기 때문에 눈앞에 벌어지는 일에만 집중할 뿐 전체적인 흐름을 파악하지 못해요. 이제 중요한 일이나 경기가 있을 때, 먼저 가서 그곳을 살펴봐요. 나는 어떻게 움직여야 할지, 일어날 수 있는 경우의 수는 무엇이며, 나는 어떻게 대응할지를 미리 생각해 두세요. 그래야만 당황하지 않고 잘 대처할 수 있으니까요.▶ 한마디 속 한자 - 致(치) 이르다, 보내다, 부르다, 끌어들이다▷ 납치(拉致) : 강제 수단을 써서 억지로 데리고 감.▷ 언행일치(言行一致) : 말과 행동이 하나로 들어맞음. 또는 말한 대로 실행함.허시봉 < 송내고 교사 hmhyuk@hanmail.net >
-
교양 기타
에어컨이 인구 대이동을 불러왔다
두바이, 방콕, 리우데자네이루…. 이들 도시의 공통점은 무엇일까요? 하나는 현재 세계 전역에서 급속히 성장 중인 대도시라는 것이고, 또 하나는 열대 기후권에 위치해 있다는 겁니다. 20세기 후반까지 세계에서 가장 큰 도시는 온대 기후권에 있었습니다. 예컨대 런던과 파리, 뉴욕과 도쿄가 그렇죠.그렇다면 그 사이 어떤 변화가 있었던 걸까요? 사람이 살 수 없었던 사막이나 열대기후에서 대도시가 출현하게 된 것은 에어컨 덕분입니다. 냉기(冷氣)를 이용해 온도와 습도를 조절할 수 있게 되면서 전 세계 거주 문화가 달라졌고 인류의 대이동이 가능해진 것이죠.인공적으로 얼음을 만드는 기술이 발명되고 나서 냉방이 가능해지고 음식을 신선하게 보관할 수 있게 됐다는 사실은 누구나 짐작할 수 있죠. 하지만 혁신적 아이디어는 우리가 생각했던 것보다 훨씬 더 큰 변화를 이끌어냅니다. 그러면 냉동기술의 발전이 우리 삶에 미친 영향을 살펴볼까요.호수의 얼음을 팔아 갑부가 된 남자1843년 미국 보스턴에서 한 남자가 얼어붙은 호수의 물을 열대 지역에 팔아 떼돈을 벌 생각을 합니다. 19세기 미국판 봉이 김선달이라 할 만한 그는 프레더릭 튜더였습니다. 얼음을 전 세계에 판매하겠다는 그의 아이디어는 사람들의 비웃음을 샀고 초반에는 사업도 고전을 면치 못했습니다.15년 뒤 얼음 무역은 흑자로 돌아서고 한 세기가 채 되지 않아 얼음은 필수품이 됩니다. 따뜻한 겨울이 닥칠 때마다 신문에서 ‘얼음 기근’을 걱정하는 기사를 쓸 정도였지요. 이후 자연에서 채취한 얼음을 이용한 냉각은 미국 사회의 지형을 바꿔놓게 됩니다.당시 시카고에는 가축을 도살해
-
학습 길잡이 기타
태양복사와 지구복사평형 2
-
학습 길잡이 기타
서울과학고 김국인 쌤의 재미난 수학세계-배시원 쌤의 신나는 영어여행
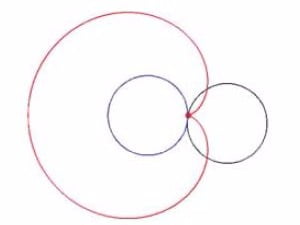
서울과학고 김국인 쌤의 재미난 수학세계 - 두개의 원으로 그리는 하트 모양 곡선반지름이 같은 두 원이 있는데, 그 중 한 원을 다른 원 주위로 굴릴 때 원 위의 한 점의 자취는 <그림1>과 같이 하트 모양의 곡선이 된다. 수학자들은 이 곡선을 cardioid라 부르는데, 그리스어로 ‘심장 모양’이라는 뜻이다. (번역을 염통 곡선이라고 한다.)원의 반지름의 길이가 α일 때, 이 곡선은 <수식1>과 같이 매개화하여 나타낼 수 있고, 직교좌표계에서는 t를 소거하여 <수식2>와 같이 나타낼 수 있다. 원을 직선 위를 굴릴 때, 원 위의 한 점의 자취를 사이클로이드라 하고 원을 다른 원의 내부[외부]에서 굴릴 때 원 위의 한 점의 자취를 하이퍼사이클로이드[에피사이클로이드]라고 한다. 염통 곡선은 에피사이클로이드의 하나인데, 두 원의 반지름의 비에 따라 뾰족한 정점(cups)의 개수가 결정된다.염통곡선은 두 원의 반지름 길이가 같으므로 정점이 하나인 에피사이클로이드이다. 염통 곡선에 대해 알려진 여러 가지 성질을 살펴보면 다음과 같다.① 염통 곡선으로 둘러싸인 부분의 넓이는 원의 넓이의 6배, 즉 6πα²이다. (적분을 통해 <수식3>과 같이 쉽게(!) 구할 수 있다.)② 염통 곡선의 길이는 반지름의 16배, 즉 16α이다. 역시 적분을 이용하여 <수식4>와 같이 구할 수 있다.③ 염통 곡선위의 한 점에서의 접선은 정점과 접점을 이은 직선과 서로 수직이다.④ 임의의 기울기에 대하여 그 기울기를 갖는 접선이 3개 존재하고, 각각의 접점을 정점과 이으면 세 선분이 이루는 각은 120º가 된다.염통 곡선을 이용하여 다음과 같이 하트를 만들 수 있다. 한 원의 원주 위에
-
학습 길잡이 기타
스스로 크다고 내세우는 것은 진정 크다고 할 수 없다 - 장자
『장자』의 ‘서무귀’편에 실려 있는 글로, “잘 짖는다고 좋은 개라 할 수 없고, 말을 잘한다고 현명한 사람이라 할 수 없는데 하물며 크다고 할 수 있겠는가? 무릇 스스로 크다고 내세우는 것은 진정 크다고 할 수 없는데 하물며 덕을 갖추었다고 할 수 있겠는가?”의 일부예요.스스로 큰일을 해내고 나면 너무 자랑하고 싶어져요. 오죽하면 말하고 싶어 참기 어려울 때, 입이 근질거린다는 표현을 하겠어요.그런데 막상 내 입으로 자랑하고 나면 마음이 참 공허해요. 생각보다 상대방의 반응도 시원찮을 때가 많고요. 그러니 이제 괜한 자랑으로 시기와 질투를 받지 말고, 조용하게 더 큰 계획을 세우세요.▶ 한마디 속 한자 - 以(이) ~로써, ~에 의해서, ~때문에▷ 이래(以來) : 지나간 어느 일정한 때로부터 지금까지. 또는 그 뒤.▷ 이이제이(以夷制夷) : 오랑캐로 오랑캐를 무찌른다는 뜻으로, 한 세력을 이용하여 다른 세력을 제어함을 이르는 말.허시봉 < 송내고 교사 hmhyuk@hanmail.net >
-
학습 길잡이 기타
"공신력있는 대회, 실전에 대비할 수 있는 기회"
고3 인문계 대상과 고3 자연계 대상은 모두 고양외고에 돌아갔다. 고3 인문계 대상은 김민선 양이, 자연계 대상은 김수한 군이 각각 차지했다. 김 양은 “여러 신문기사나 인터뷰 특집기사 뿐만 아니라 책을 꾸준이 읽고 글을 성심성의껏 썼던 경험이 밑바탕이 되었다”며 수상 소감을 밝혔다. 김 군은 “참고서의 해설지처럼 답을 논리적으로 써내려 가려 노력하고 수학 논문을 읽어왔던 것이 도움이 되었다”고 했다.김 양은 “미디어에 대한 제시문은 익숙했지만 제시문에 대한 분석과 통계자료에 대한 해석을 함께 해야 한다는 점에서 다소 어려웠다”고 평가했다. 김 군은 “피보나치 수열과 증명문제가 어려웠지만 롤의 정리, 미적분을 이용한 자취의 길이 등의 문제는 여러번 접해와 큰 무리는 없었다”고 했다.‘그린나래’ 잡지부장을 하고 있는 김 양은 “교내 잡지를 출간할 뿐만 아니라 영문시사잡지인 NE Times에 기사를 실으면서 기자의 꿈을 키워가고 있다”고 했다. 장차 수학과 관련된 일을 하고 싶다는 김 군은 “수학이 많은 학생들에게 큰 걸림돌로 작용할텐데 논리적으로 생각하는 연습을 하고 희망을 갖고 노력했으면 좋겠다”고 말했다.두 수상자는 이구동성으로 “생글논술대회는 공신력이 있는 대회”라며 “향후 대입 논술전형이라는 실전에 대비할 수 있는 좋은 기회였다”고 덧붙였다.---------------------------------------------------------제19회 생글논술경시대회 수상자 명단(가나다순)▶고1공통 유형 대상(1명) : 상패, 상장, 장학금 30만원 △정지원(동두천외고)최우수상(1명) : 상패, 상장, 장학금 20만원 △이정민(안양외고)우수상(10명) :
-
학습 길잡이 기타
서울과학고 김국인 쌤의 재미난 수학세계-배시원 쌤의 신나는 영어여행
서울과학고 김국인 쌤의 재미난 수학세계 - 식물의 이름에서 딴 마름모학교 선생님들과 대화하던 중 마름모에 대해 설명할 기회가 생겨 마름모란 ‘마름’이란 식물의 잎 모양의 사각형이라 말하자 모두 깜짝 놀라며 처음 듣는 이야기라며 신기해하였다. 수학 용어는 대부분 용어의 뜻을 포함하고 있어 용어를 잘 이해하면 개념을 바로 형성할 수 있다. 하지만 마름모와 같이 어떤 경우에는 그 뜻을 이해하지 못한 채 기계적으로 암기하고 있는 경우도 있다. 마름모는 네 변의 길이가 같은 사각형으로 영어로는 rhombus 또는 diamond라 한다. 마름모는 마름의 잎 또는 열매 모양이라는 뜻으로 한자 능형(菱形)을 우리말로 옮긴 것인데, 사다리꼴과 같이 마름꼴이라 하지 않고 마름모라고 옮긴 것도 약간 의문이지만 식물 마름과는 아무 상관없이 또 아무 의심없이 전적으로 수학 쌤을 믿으며 약간 마름모에 대해 공부해 왔던 것이다. 어떤 나라에서는 의미 그대로 ‘등변사각형’이라고 하기도 한다.한 쌍의 변이 서로 평행인 사각형을 ‘사다리꼴’이라 하는데 이는 제형(梯形)을 우리말로 옮긴 것이다. 서로 마주 대하는 두 쌍의 변이 각각 평행인 사각형을 평행사변형(平行四邊形)이라고 하는데 이를 우리말로 옮기면 ‘나란히꼴’이다. 각각의 용어를 통일성 있게 마름꼴, 사다리꼴, 나란히꼴이라고 정하지 못한 점이 약간 아쉽다.수학 용어 대부분은 한자어를 그대로 사용하고 있어 한자에 익숙한 사람에게는 의미가 있지만 그렇지 못한 경우 무의미하게 외우는 수밖에 없어 수학을 공부하는 데 어려움을 겪는 경우가 많다. 로그 단원에서 어려운 문제로 ‘지표와 가수&rsqu
-
학습 길잡이 기타
길을 잃었다는 것은 갈 길을 묻지 않았기 때문이고, 물에 빠졌다는 것은 건널 물길을 묻지 않았기 때문이다. - 순자
『순자』의 ‘대략’편에 실려 있는 글로, “천하에는 나라마다 뛰어난 인물도 있고, 시대마다 현인(賢人)도 있다. 길을 잃었다는 것은 갈 길을 묻지 않았기 때문이고, 물에 빠졌다는 것은 건널 물길을 묻지 않았기 때문이다. 몸을 망친 사람은 (대체적으로) 독선을 좋아하기 때문이다.”의 일부예요.당신은 지금 어디에 있나요? 고개를 돌려 한번 살펴보세요. 혹시 길을 잃거나 물에 빠지지 않았나요? 그런데 왜 혼자만 끙끙 앓고 있나요? 믿을 만한 사람에게 도움을 청하거나, 방법을 아는 사람에게 물어보세요. 그런 다음 그 답 중에 가장 나은 것을 선택하세요. 어차피 그곳에 혼자 있어봐야 뾰족한 답도 없잖아요.▶ 한마디 속 한자 - 路(로) 길, 도리(道理)▷ 애로(隘路) : 1. 좁고 험한 길. 2. 어떤 일을 하는 데 장애가 되는 것.▷ 격화일로(激化一路) : 격렬하게 되는 과정.허시봉 < 송내고 교사 hmhyuk@hanmail.net >