학습 길잡이 기타
-
학습 길잡이 기타
화학·지구과학
-
학습 길잡이 기타
서울과학고 김국인 쌤의 재미난 수학세계-배시원 쌤의 신나는 영어여행
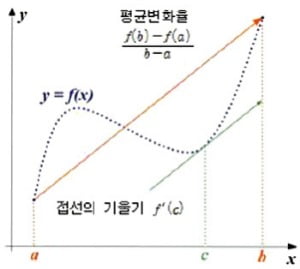
서울과학고 김국인 쌤의 재미난 수학세계 - 적분은 면적에서, 미분은 접선에서 출발미적분학에서 평균값 정리(mean value theorem)의 중요성을 강조하기 위해 ‘MVT is the MVT!(Mean value theorem is the most valuable theorem!)’라는 문장이 있다. 미적분학에서 가장 중요한 정리는 수식1과 같다. 적분은 면적 문제에서, 미분은 접선 문제에서 시작돼 출발점이 서로 다른 두 개념 사이의 관계를 설명하는 정리이기 때문이다. 미적분학의 기본정리를 증명할 때 평균값 정리가 사용된다는 점만 보더라도 미적분학에서 평균값 정리가 갖는 의미를 알 수 있다. 물론 이외에도 평균값 정리의 활용이나 확장은 미적분학 도처에서 찾을 수 있다.평균값 정리는 함수 f(x)가 닫힌 구간[a,b]에서 연속이고 열린 구간 (a, b)에서 미분 가능일 때 수식 2를 만족하는 c가 열린 구간 (a, b)에 적어도 하나 존재한다는 것을 의미한다. 그래프를 통해 해석해 보면 좌표평면에서 두 점 (a, f(a)), (b, f(b))를 잇는 직선의 기울기와 평행한 접선이 존재한다는 의미다. 만약 f(a)=f(b)이면 구간[a,b]에서 기울기가 0인 접선이 존재한다는 것으로 이를 롤(Rolle)의 정리라 한다. (LoL이 아니다!)롤의 정리를 증명해보면 함수 f(x)가[a,b]에서 연속이고 (a, b)에서 미분가능하며 f(a)=f(b)이다. 먼저 구간[a,b]에서 f(x)가 상수함수인 경우 (a, b) 안의 모든 x에 대하여 f' (x)=0 이다. f(x)가 상수함수가 아닌 경우 f(x) > f(a)인 x가 존재한다고 하면 f(x)가[a,b]내부에서 최댓값을 갖게 된다. x=c에서 최댓값을 갖게 된다. x=c에서 최댓값을 갖는다고 하면 미분가능성과 극한의 성질에 의해 수식3이므로 f' (c)=0 이 된다.이제 롤의 정리를 이용해 평균값 정리를 증명해보
-
학습 길잡이 기타
사람의 마음은 변하기 쉽고, 인생길은 험하다 - 채근담
『채근담』에 실려 있는 글로, “사람의 마음은 변하기 쉽고, 인생길은 험하다. 가기 어려운 길은 모름지기 한 걸음 물러설 줄 알아야 하고, 가기 쉬운 길은 10분의 3을 양보할 줄 알아야 한다.”의 일부예요.마음이라는 것은 덥고 차갑고를 반복해요. 사람에게든 물건에게든 말이죠. 게다가 평탄하게만 살기 어려운 것이 세상이에요. 그래서 사람들이 세상을 그리 조심스럽게 사는지도 몰라요.채근담은 말하고 있어요. 어려운 일을 만나면 한 발 물러나 신중하게 몸을 움직이고, 쉬운 일을 만나면 홀로 공을 차지하지 말고 다른 사람과 나누라고 말이죠. 아마 이리 살다보면 남들보다 험한 상황을 덜 당하게 되고, 주변에 나를 좋아하는 사람이 많아질 거예요.▶ 한마디 속 한자 - 路(로) 길, 도리(道理)▷ 애로(隘路) : 좁고 험한 길. 어떤 일을 하는 데 장애가 되는 것.▷ 노류장화(路柳牆花) : 아무나 쉽게 꺾을 수 있는 길가의 버들과 담 밑의 꽃이라는 뜻으로, 기생을 비유적으로 이르는 말.허시봉 < 송내고 교사 hmhyuk@hanmail.net >
-
학습 길잡이 기타
역함수의 미분법
-
학습 길잡이 기타
서울과학고 김국인 쌤의 재미난 수학세계-배시원 쌤의 신나는 영어여행
서울과학고 김국인 쌤의 재미난 수학세계 - 미분가능과 연속함수 y=f(x)가 x=α에서 극한값과 함수값이 모두 존재하고 그 값이 같을 때 x=α에서 함수 y=f(x)가 연속이라고 한다. 즉 수식1과 같으면 y=f(x)는 x=α에서 연속이다. 거꾸로 말하면 x=α에서 함수값 또는 극한값이 존재하지 않거나 두 값이 존재하더라도 일치하지 않으면 x=α에서 불연속이다. 고등학교 수준에서 연속성 문제를 해결하기 위해서는 x=α에서 좌극한과 우극한이 모두 함수값이 되는 것을 보여주면 된다.또 함수 y=f(x)가 x=α에서 연속이면 α에 수렴하는 x의 수열에 대하여 수식2와 같이 수렴한다.그럼 모든 실수에서 불연속인 함수가 있을까? 독일의 수학자 디리클레(Dirichlet)는 다음과 같은 함수(수식3)를 제시했다. x가 유리수 값만을 가지면서 x→α인 경우 f(x)→1이고 x가 무리수 값만을 가지면서 x→α인 경우 f(x)→0이므로 이 함수는 x=α에서 불연속이다. 이 함수를 다음 수식 4와 같이 표현할 수도 있다.디리클레 이전에 함수는 두 변수 사이의 종속 관계를 나타내는 수학적 개념으로 여겨졌으나, 디리클레 함수의 등장으로 두 변수 사이의 대응이라는 추상적 개념으로 함수를 다루기 시작하게 됐고, 이후 엄밀한 함수의 정의를 바탕으로 해석학이라는 학문이 태어났다.한편 함수 y=f(x)에 대하여 극한(수식5)이 존재하면 x=α에서 미분가능하다라고 한다. 그리고 이 값을 x=α에서 미분계수 f‘(α)라 한다. 미분가능성과 연속성 사이에는 어떤 관계가 있을까? 바로 ‘간.미.연’이다. 즉 간단히 말해 미분가능이면 연속이다. (기억하기 쉽죠?^^) 이는 다음의 극한 성질(수식6)을 이용
-
학습 길잡이 기타
사람은 백년도 못살면서, 항상 천년의 근심을 안고 사네 - 태평어람
『태평어람』에 있는 글로, “고시(古詩)에 이르기를 사람은 백년도 못 살면서, 항상 천년의 근심을 안고 사네. 낮이 짧고 괴로운 밤이 기니, 어찌 촛불을 잡고 놀지 않으랴”의 일부예요. 그러고 보니 우리는 하루 중 많은 시간을 걱정과 근심으로 보낸다는 것을 알 수 있어요.시인은 우리에게 평소에 하는 걱정을 10분의 1로 줄이고, 그렇게 남은 10분의 9의 시간을 즐겁게 살라고 조언하고 있어요. 그러니 이제 걱정하고 염려하느라 시간과 마음을 너무 소비하지 마세요. 차라리 그 시간에 즐겁고 의미 있는 일을 찾으세요. 그래도 돼요. 아셨죠?▶ 한마디 속 한자 - 載(재) : 싣다, 타다, 해, 년(年)▷ 등재(登載) : 1. 일정한 사항을 장부나 대장에 올림. 2. 서적이나 잡지 따위에 실음.▷ 천재일우(千載一遇) : 천 년 동안 단 한 번 만난다는 뜻으로, 좀처럼 만나기 어려운 좋은 기회를 이르는 말.허시봉 < 송내고 교사 hmhyuk@hanmail.net >
-
학습 길잡이 기타
화학평형
-
학습 길잡이 기타
서울과학고 김국인 쌤의 재미난 수학세계-배시원 쌤의 신나는 영어여행
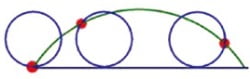
서울과학고 김국인 쌤의 재미난 수학세계 - ‘카발리에리 원리’ 이용해 넓이 구하기반지름이 r인 원을 x축 위로 한 바퀴 굴렸을 때 원점과 겹치는 점이 그리는 곡선 식(수식 1)과 x축으로 둘러싸인 부분의 넓이를 구해보자.적분을 이용해 문제 풀이를 하면 수식 2이므로 치환적분을 이용하여 구하는 넓이는 수식 3과 같다. 간결하고 멋진 풀이지만 적분을 사용하여 구한다는 자체가 큰 부담이 된다. 이번에는 적분 계산 없이 넓이를 구할 수 있는 방법인 카발리에리(Cavalieri)의 원리를 소개한다. 17세기 이탈리아 수학자 카발리에리는 그의 저서 <불가분량의 기하학>에서 구의 부피를 구하는 원리로 이 원리를 제시하였다. 카발리에리의 원리란 단면의 비가 일정하면 전체의 비도 같다는 것으로 평면도형의 넓이나 공간도형의 부피를 구하는 데에 응용할 수 있다.두 개의 평면도형[공간도형]이 한 쌍의 평행선[평행면] 사이에 끼어 있고 그 평행선[평행면]들과 임의의 선[면]으로 그 두 평면도형[공간도형]을 잘랐을 때 생기는 두 선분[단면]의 길이[넓이]가 항상 일정한 비를 가지면, 두 평면도형[공간도형]의 넓이[부피]도 또한 그 비를 갖는다.예를 들어 x축에 평행한 선으로 타원(수식4)과 원(수식5)을 잘라보면 잘린 선분의 길이 비는 a:b이다. 즉 타원에 의해 잘린 설분의 길이가 항상 원에 의해 잘린 선분의 길이의 a/b배이므로 타원의 넓이는 원의 넓이의 a/b배인 a/b × πb²= πab가 된다. 이제 카발리에리의 원리를 이용하여 문제를 풀어보자. 구하는 부분을 반으로 나누어 뒤집어 붙인 상태인 그림 3을 생각해보자.공통 부분과 원의 넓이가 카발리에리의 원리에 의해 넓이가 같아지는 것을 알