학습 길잡이 기타
-
학습 길잡이 기타
서울과학고 김국인 쌤의 재미난 수학세계-배시원 쌤의 신나는 영어여행
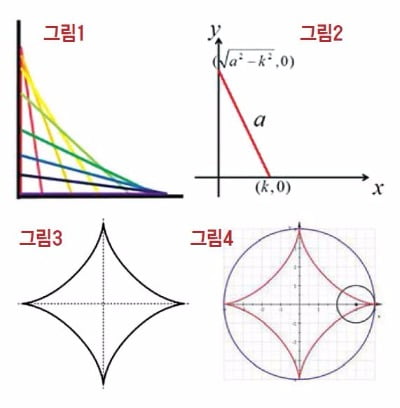
서울과학고 김국인 쌤의 재미난 수학세계 - 저상버스 출입문과 아스트로이드저상버스는 타고 내릴 때 계단 없이 탈 수 있어 교통약자들이 이동하기에 편리하다. 저상버스의 뒷문은 안쪽으로 미끄러지며 열리는 구조로 돼 있는데 이런 문을 ‘글라이딩 도어’라고 한다. 슬라이딩 도어와 비교해 자리를 적게 차지하지만, 안쪽으로 열릴 때 문에 부딪힐 수 있으므로 조심해야 한다. 저상버스의 글라이딩 도어가 열리고 닫힐 때 문이 쓸고 지나간 부분은 어떤 모양일까?버스 바닥을 좌표평면이라 생각하면 이 좌표평면 위에서 문은 길이가 a로 일정한 선분이 될 것이고, 선분의 한쪽 끝은 x축 위를 움직이고 다른 쪽 끝은 y축 위를 움직인다. 이때 선분이 쓸고 지나간 부분의 모양<그림1>을 구하는 문제로 바꿀 수 있다.<그림2>에서 문이 x축과 만나는 점이 (k, 0)이면 y축과 만나는 점은 (0, √a²-k²) <수식 1>로 나타낼 수 있다. 문이 쓸고 간 부분의 둘레의 곡선은 x를 고정할 대, y의 최댓값으로 이뤄진 곡선이므로 <수식1>을 k에 관해 미분하면 <수식2>와 같다. 따라서 <수식3>의 x를 <수식1>에 대입하면 <수식4>이고 <수식3과 4>에서 k를 소거하면 <수식5>가 된다. 그래프는 <그림3>과 같은 별 모양의 도형이다. 이 도형의 이름은 ‘아스트로이드(astroid)’이고 요한 베르누이와 라이프니츠가 처음으로 연구했다.이 도형은 일전에 연구한 사이클로이드와도 관련이 있다. <그림4>와 같이 원 내부에서 작은 원이 구를 때 작은 원 위의 한 점의 자취를 ‘하이퍼사이클로이드’라 하는데, 작은 원의 반지름(r)과 큰 원의 반지름(R)의 비가 1:4일 경우
-
학습 길잡이 기타
대개 좋은 물건은 견고하지 못하다 - 전당시
중국 당나라 때 시인 ‘백거이’의 ‘간간음(簡簡吟)’에 있는 구절로, “대개 좋은 물건은 견고하지 못하니, 채색 구름은 쉽게 흩어지고 유리는 부서지기 쉽다”의 일부예요.사람들은 가인박명(佳人薄命)이란 말을 두고 세상이 가인(佳人)을 시기해서 그가 평탄하게 살지 못한다고 해요. 그런데 그 이유가 꼭 사람들의 시샘 때문일까요?가인(佳人)은 뛰어난 능력과 예쁜 용모로 모두의 관심을 받아요. 하지만 그들은 그 능력과 용모만 믿다가 세상을 사는데 중요한 부분을 자주 놓치곤 하죠. 그리고 잘못 되었을 때 자신의 아름다움을 시샘한 세상 때문이라고 한탄해요.이제 남 탓하지 마세요. 스스로 강해져야 해요.▶ 한마디 속 한자 - 堅(견) 굳다, 단단하다, 갑옷▷ 견과(堅果) : 단단한 껍데기와 깍정이에 싸여 한 개의 씨만이 들어 있는 나무 열매를 통틀어 이르는 말. 도토리, 밤, 은행, 호두 따위가 있다.▷ 견여금석(堅如金石) : 서로 맺은 언약이나 맹세가 금석과 같이 단단함을 이르는 말.허시봉 < 송내고 교사 hmhyuk@hanmail.net >
-
학습 길잡이 기타
서울과학고 김국인 쌤의 재미난 수학세계-배시원 쌤의 신나는 영어여행
서울과학고 김국인 쌤의 재미난 수학세계 - 케빈 베이컨의 6단계 법칙과 에어디시 넘버중동호흡기증후군(메르스·MERS)가 확산되면서 매일 확진 환자가 몇 명인지 2차 감염인지 3차 감염인지 보도에 촉각을 세우고 있다. 중동에 가본 적도 없고, 낙타를 본 지 10년도 넘었지만 메르스 바이러스 확산에 걱정하는 것을 보면 인간은 사회적 동물이라는 아리스토텔레스의 주장이 떠오른다.사람과 사람 사이의 관계가 얼마나 가까운지에 대한 것으로 케빈 베이컨의 6단계 법칙이라는 관계법칙이 있다. 1994년 미국에서 한 TV 토크쇼 ‘존 스튜어트 쇼’를 보던 3명의 대학생이 ‘배우 케빈 베이컨이 모든 사람을 아는 우주의 중심이라는 것을 입증할 수 있다’는 내용의 편지를 방송국에 보내고 이에 흥미를 느낀 방송사가 이들을 베이컨과 함께 출연시켰다.이 세 사람은 청중이 이름을 대는 배우들이 베이컨과 어떻게 연결되는지 입증했는데 예를 들면 배우 해리슨 포드는 캐런 앨런과 영화 ‘레이더스’에 함께 출연했고 앨런은 베이컨과 ‘애니멀 하우스’에서 주연을 맡았으므로 한 단계만 건너면 인연이 있다는 식이다. 이를 계기로 미국에서는 ‘케빈 베이컨 게임’이 유행하게 된다. 영화에 함께 출연한 관계를 1단계로 설정하고 배우들이 케빈과 몇 단계 안에 연결될 수 있는지를 빨리 찾는 게임인데, 놀랍게도 거의 모든 배우가 6단계 안에 케빈과 연결됐다.수학에서는 네트워크의 특성을 보여주는 예로 ‘에어디시 넘버’라는 게 있다. 헝가리의 수학자 폴 에어디시는 수백 명의 다른 수학자와 공동으로 연구해 조합론, 그래프 이론, 정수론 등에서 방대한 업
-
학습 길잡이 기타
매개변수 방정식과 도형의 변환
-
학습 길잡이 기타
바람이 지나가면 대나무 숲은 소리를 남겨 두지 않는다. - 채근담
『채근담』에 실려 있는 글로, “바람이 성긴 대나무 숲에 불어와도 바람이 지나가면 대나무 숲은 소리를 남겨 두지 않고, 기러기가 찬 연못을 지나도 기러기가 지나가면 연못은 그림자를 남겨 두지 않는다. 그러므로 군자는 일이 오면 비로소 마음이 나타나고, 일이 지나가면 마음도 그와 함께 공(空)으로 돌아간다.”의 일부예요.감추려고 해도 잘 드러나는 감정이 ‘화’예요. 이 ‘화’는 세상과 타인이 내 맘처럼 움직여주지 않을 때 생겨나 우리의 몸과 마음을 병들게 해요. 그러니 이제 세상과 타인을 내 마음대로 하려 하지 마세요.바람이 불어오면 함께 흔들리고, 바람이 지나가면 보내주세요. 사람이 다가와 나를 흔들면 흔들리다가도, 그 사람이 떠나가면 보내주세요.▶ 한마디 속 한자 - 聲(성) 소리, 이름, 선언하다▷ 성명(聲明) : 어떤 일에 대한 자기의 입장이나 견해 또는 방침 따위를 공개적으로 발표함. 또는 그 입장이나 견해.▷ 허장성세(虛張聲勢) : 실속은 없으면서 큰소리치거나 허세를 부림.허시봉 < 송내고 교사 hmhyuk@hanmail.net >
-
학습 길잡이 기타
지구과학 : 태양복사와 지구복사 평형
-
학습 길잡이 기타
서울과학고 김국인 쌤의 재미난 수학세계-배시원 쌤의 신나는 영어여행
서울과학고 김국인 쌤의 재미난 수학세계 - 미분과 적분의 오작교미적분학은 극한, 함수, 무한급수, 미분, 적분 등을 다루는 수학의 한 분야다. 미분은 어떤 지점에서 접선을 구하는 문제인데, 이를 이용해 복잡한 함수를 선형으로 근사해 다루기 쉬운 형태로 파악할 수 있다. 적분은 넓이를 구하는 문제로, 국소적으로 구한 넓이의 합을 이용하는 구분구적법이 모태가 된다. 기울기를 구하는 미분과 넓이를 구하는 적분은 완전히 다른 별개의 두 개념이지만 밀접한 관련을 갖는데 미적분학의 기본정리가 그에 대한 내용이다. 견우와 직녀가 칠월 칠일 칠석날 오작교를 건너 만나듯 미분과 적분은 미적분학의 기본정리(FTC)를 통해 만나게 되는 것이다.함수 f(x)와 x축, 직선 x=a, x=b로 둘러싸인 부분의 넓이를 구분구적법으로 구하면 [수식1]과 같다. 함수 f(x)가 [a, b]에서 연속이면 [수식 1]의 무한급수는 수렴하는데, 이때 값을 a에서 b까지 함수 f(x)의 정적분이라고 하고 기호로 [수식2]로 나타낸다.함수 f(x)를 적분하려면 [수식1]의 무한급수의 합을 구하면 되는데, 단순히 넓이를 구하는 문제에서 발전해 수학자들은 넓이의 변화에 관심을 갖게 된다. [수식 3]으로 넓이 함수를 정의하면 f(x)가 [a, b]에서 연속인 경우 S(x)는 미분가능하고 S’(x)=f(x)이다. 이것이 첫번째 미적분학의 기본정리이다. [수식 4]필자는 수학책에 나오는 여러 수식 중 가장 아름다운 수식이라 생각한다. 미분과 적분의 관계에 관한 설명이기 때문이다. 적분한 함수를 미분하면 원래 함수가 된다. 즉 미분과 적분이 서로 역연산 관계로 만나게 되었다. 다음으로 두 번째 미적분학의 기본정리를 만나 보자.F’(x)=f(x)인 F(x)를 f(x)의 원시
-
학습 길잡이 기타
모든 곳을 지키려고 하면 모든 곳이 약해진다. - 손자병법
『손자병법』‘허실’편에 실린 글로, “아군이 진격할 곳을 적이 모르게 해야 한다. 적이 이를 모르면 방비해야 할 곳이 많아진다. 방비할 곳이 많아지면 아군이 상대할 적의 병력은 줄어든다. (중략) 모든 곳을 지키려고 하면 모든 곳이 약해진다. 이리되면 병력이 적은 자는 막으려는 적이 되고, 병력이 많은 자는 막게 한 아군이 된다”의 일부예요.믿을 만한 사람에게는 속내를 털어놓아도 좋지만, 싸워야 하는 상대에게는 결코 자신의 의중을 드러내지 마세요. 나보다 강한 상대일수록 더더욱 말이죠. 그냥 상대하기도 버거운데 내 마음을 미리 알고 준비한 상대는 또 얼마나 강하겠어요.이제 마음속 비장의 카드 한 장은 잘 감추세요.▶ 한마디 속 한자 - 寡(과) 적다, 약하다▷독과점(獨寡占) : 독점과 과점. 개인이나 하나의 단체가 다른 경쟁자를 배제하고 생산과 시장을 지배해 이익을 독차지하거나 몇몇 기업이 어떤 상품시장의 대부분을 지배하는 상태.▷중과부적(衆寡不敵) : 적은 수효로 많은 수효를 대적하지 못함.허시봉 < 송내고 교사 hmhyuk@hanmail.net >