학습 길잡이 기타
-
학습 길잡이 기타
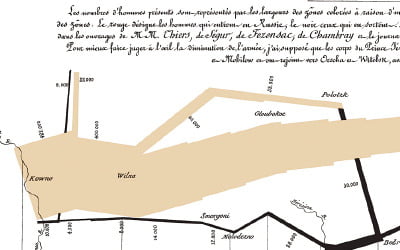
데이터로 역사 알려주는 '나폴레옹 진군 맵'
지난 생글생글 916호, 919호의 ‘재미있는 수학’에서 역사적으로 의미가 있는 창의적인 그래프의 사례를 알아보았습니다. 이번에는 마지막으로 프랑스의 황제 나폴레옹의 진군 맵 이야기를 소개합니다.1812년 여름, 유럽을 제패한 나폴레옹의 제국은 막강했지만, 러시아의 독자적 행보는 그의 자존심을 자극했습니다. 나폴레옹은 영국을 압박하기 위해 1806년 유럽 대륙과 영국의 통상을 금지하는 대륙봉쇄령을 내렸는데, 러시아 황제 알렉산드르 1세가 영국과의 무역을 재개하자 나폴레옹은 이를 대륙봉쇄령에 대한 명백한 배신으로 간주했습니다. 결국 응징이라는 명분 아래 나폴레옹은 군대를 이끌고 러시아로 향하는, 역사상 가장 대규모의 원정을 시작했습니다.당시 나폴레옹이 이끌던 총병력은 60만 명으로, 유럽 동북부와 중부에 있던 프로이센으로부터 2만 명, 오스트리아로부터 6만 명을 지원받았습니다. 하지만 그는 러시아의 지형과 기후, 그리고 러시아인의 끈질긴 전략을 과소평가했습니다. 러시아군은 정면 대결 대신 후퇴를 택했고, 퇴각하는 길마다 마을과 농지를 불태웠습니다. 이른바 ‘초토화 전략’이었습니다. 프랑스 연합군의 말들은 사료가 없어 떼죽음을 당했습니다. 이에 말이 이끌던 보급 마차들은 본대(本隊)를 따라잡지 못하게 되어 병사들은 부대를 이탈해 식량을 찾아 헤맸습니다. 보급로는 끊겼고, 프랑스 연합군은 스스로 굶주림과 추위 속에 고립되고 말았습니다.1812년 9월 14일, 마침내 프랑스 연합군은 모스크바에 입성했습니다. 그러나 승리의 기쁨은 오래가지 않았습니다. 도시 전체가 불길에 휩싸였던 것입니다. 러시아인들은 점령당하느니 스스로 도시를 불
-
학습 길잡이 기타
수많은 입체도형의 부피 계산하는 강력한 무기
자, 10원짜리 동전 10개를 반듯하게 쌓아 올린 동전 탑이 있습니다. 누군가가 실수로 이 탑의 중간을 툭 쳐서 옆으로 비스듬히 밀어버렸다고 상상해봅시다. 모양은 삐뚤어졌지만, 이 기울어진 동전 탑의 부피는 처음에 반듯했을 때와 비교해 어떻게 변했을까요?1. 증가한다. 2. 감소한다. 3. 그대로다.일렬로 쌓은 동전탑이 차지하는 부피가 왠지 더 작아 보입니다. 하지만 정답은 3번입니다. 동전을 옆으로 밀었을 뿐, 동전의 개수가 늘어나거나 크기가 변한 것은 아니니까요. 모양은 변했어도 그 안을 채우고 있는 내용물의 양(부피)은 여전히 ‘10원짜리 10개’ 그대로기 때문입니다.지금 질문한 것이 큰 수학의 개념을 다지기 위한 원리라고 한다면 믿어지나요?이 당연해 보이는 현상에 수학자들은 조금 멋진 이름을 붙여주었습니다. 바로 ‘카발리에리의 원리(Cavalieri’s Principle)’입니다. 이름은 어렵게 들릴지 모르지만, 내용은 우리가 방금 동전으로 확인한 사실과 똑같습니다.“두 입체도형이 높이가 같고, 바닥과 평행한 모든 지점에서의 단면적(잘린 면의 넓이)이 서로 같다면, 두 도형의 부피는 같다.”수학자들은 이 당연한 현상을 놓치지 않고 하나의 강력한 도구로 다듬어냈습니다. 바로 정적분입니다. 어렵게 생각할 필요 없이 적분 기호의 생김새만 봐도 그 원리를 알 수 있습니다.우리가 쓰는 적분 기호 인테그랄은 합한다는 뜻을 가진 영어 단어 Sum의 첫 글자 S를 길게 늘어뜨린 모양입니다. 즉 싹 다 긁어모아서 합친다는 뜻을 담고 있죠.카발리에리의 원리를 이 기호로 표현하면 아주 단순해집니다. 우리가 동전 탑을 쌓듯이, 아주 얇은 단면의 넓이들을 바닥부터 꼭대기까지 차
-
학습 길잡이 기타
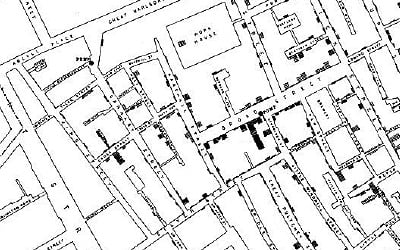
통계로 콜레라의 원인 밝혀낸 존 스노
지난 생글생글 제916호의 ‘재미있는 수학’에서는 플로렌스 나이팅게일의 장미 그림에 대해 알아보았습니다. 이번에는 역사적으로 의미 있는 창의적 그래프 중 장미 그림 외 다른 그래프의 사례를 알아보도록 하겠습니다.빅토리아 여왕 시대 영국의 의사이자 역학(epidemiology)의 창시자인 존 스노(John snow, 1813~1858)의 콜레라 지도 이야기입니다. 1854년 런던에서는 콜레라가 크게 유행했습니다. 콜레라는 심한 설사와 탈수 증상을 일으키는 장질환인데, 진행 속도가 매우 빨라 배앓이만 하다가 치료도 못 받고 죽을 만큼 무서운 질병이었습니다. 당시만 해도 콜레라의 발생 원인이나 치료법을 알 수 없었기에 사람들은 공포에 휩싸였습니다.영국에서는 콜레라로 인한 피해에 대해 광범위하고 체계적인 통계 조사를 시행했습니다. 이 작업은 감염병에 관한 통계조사로는 최초로 평가됩니다. 당시 조사를 맡은 의사 중 한 명인 윌리엄 파(William Farr, 1807~1883)는 통계조사를 토대로 분석한 결과 사람들이 사는 지대의 높이가 낮을수록 사망률이 높다고 봤습니다. 당시 런던은 세계에서 가장 큰 도시였는데, 하수 시설이 제대로 구축되어 있지 않아 오염된 물이 템스강으로 흘러들어 강물에서 심한 악취가 났습니다. 그래서 템스강에서 나는 악취가 콜레라의 원인일 것이라고 판단했습니다. 윌리엄 파는 본인 나름대로 데이터를 철저히 분석했지만, 콜레라의 원인을 잘못 짚었습니다.존 스노는 병원에 오는 환자들을 보며 이상함을 느꼈습니다. 콜레라가 공기에 의해 옮겨진다고 알려져 있었지만, 환자들의 증상을 보면 공기를 통한 전염이라고 보기에는 도저히 설명되지 않았습니다. 공기를 통한 전염이라면 증
-
학습 길잡이 기타
동전 5번 연속 앞면 나왔다면 6번째는 뒷면?
우리는 어떤 일이 일어날 확률을 얼마나 잘 판단할 수 있을까요? 예를 들어 “동전을 던졌을 때 앞면이 나올 확률은 50%”라는 사실은 모두가 알고 있습니다. 하지만 실제로 다섯 번 연속 앞면이 나왔다면 여섯 번째는 뒷면이 나올 것 같다고 느끼지 않나요? 이 단순한 오해 속에 인간의 사고가 얼마나 직관에 의존하는지, 그리고 그 직관이 얼마나 자주 우리를 속이는지가 숨어 있습니다.이런 착각은 ‘도박사의 오류’라고 불립니다. 앞서 동전이 다섯 번 연속으로 앞면이 나왔다고 해서 다음에 뒷면이 나올 확률이 높아지는 것은 아닙니다. 각 시행은 서로 독립적이기 때문이죠. 매번 앞뒤의 확률은 여전히 2분의 1, 즉 50%입니다. 그런데도 우리는 마치 자연이 ‘균형’을 맞춰줄 거라 믿습니다. ‘이쯤이면 나올 때가 됐지’라는 생각은 인간의 심리적 균형 감각에서 비롯된 착각입니다.연속으로 앞면이 나올 확률은 실제로 매우 작은 건 맞습니다. 굳이 내기를 해야 했다면 ‘연속으로 앞면이 나올 경우’에 걸었어야 합니다. 그렇지만 각 시도의 확률은 여전히 2분의 1이고, ‘균형’을 위해 확률이 변하지는 않습니다. 확률은 과거를 기억하지 않으니까요.비슷한 예로, 생일의 확률 역시 우리의 직관을 배반합니다. 한 반에 학생이 23명 있을 때, 생일이 같은 학생이 있을 확률은 얼마나 될까요? 1년은 365일이고 23명의 생일이 있으니 ‘그 정도로는 겹치기 어렵겠지’라고 생각하는 경우가 많습니다. 하지만 실제 이 확률은 50%가 넘습니다. 예상보다 꽤 높은 편이죠.구체적으로 설명하자면, 23명의 생일이 모두 다를 확률을 구해보는 것이 제일 좋은 방법입니다. 첫 번
-
학습 길잡이 기타
'원뿔곡선=2차곡선'…수학언어로 짜여진 우주 비밀
고대의 수학자들이 순수한 호기심으로 발견한 이 네 가지 ‘원뿔 곡선(Conic Sections)’이 먼 훗날 A와 B라는 계수의 조건만으로 완벽하게 분류되는 ‘2차 곡선(Quadratic Curves)’과 정확히 일치한다는 사실은, 이 우주가 얼마나 수학적인 언어로 아름답게 짜여 있는지를 보여주는 매우 강력한 증거 중 하나입니다. 우리는 딱딱한 대수학의 방정식을 풀었을 뿐인데, 그 끝에서 원뿔을 자르던 고대 수학자의 빛나는 호기심과 마주하게 된 것입니다.
-
학습 길잡이 기타
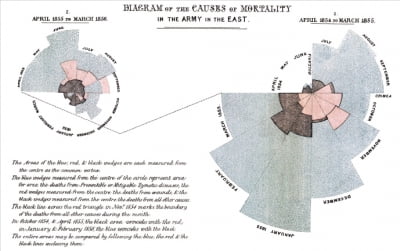
'장미 그림'으로 시각화…통계로 세상 구한 나이팅게일
데이터 시각화를 할 때 나타날 수 있는 통계 그래프는 막대그래프, 꺾은선그래프, 원그래프, 띠그래프 등의 기본적인 통계 그래프 이외에도 자료에 대한 이해와 창의적 사고를 바탕으로 다양하게 응용해서 나타낼 수 있습니다. 이번에는 역사적으로 의미가 있는 창의적인 그래프를 알아보도록 하겠습니다.설득력을 높이기 위해 창의적인 방법으로 그래프를 사용하여 그린 통계 그래프로 백의의 천사로 알려진 플로렌스 나이팅게일(Florence Nightingale, 1820~1910)의 장미 그림이 유명합니다. 나이팅게일은 1854년 4월부터 1855년 3월까지 크림전쟁(1853년 10월~1856년 3월, 크림반도에서 벌어진 전쟁)에 간호사로 참전했습니다. 그런데 그녀가 근무한 야전병원의 상태는 매우 열악했습니다. 좁은 장소에서 많은 환자가 뒤섞여 방치되었고, 불결했으며, 약품 또한 턱없이 부족했습니다. 그녀는 수많은 부상병과 사망자를 보며 병원에 들어올 당시 부상 원인과 죽었을 때 사망 원인이 다르다는 사실을 발견했습니다. 나이팅게일은 우선 환자들의 부상 정도와 상태를 매일 기록했고, 사망자에 대해서도 원인과 내역을 기록하며 분석했습니다.매일 기록된 데이터를 참고해 사망 원인을 분석해보니 대부분이 병원균 감염이었습니다. 나이팅게일은 전염병을 예방하려면 환경 개선이 우선이라고 생각했습니다. 그런데 환경을 개선하려면 이를 결정하고 실행하는 행정관을 설득해야 했습니다. 나이팅게일은 관료적인 그들을 설득하기 위해 자료를 살폈습니다. 환자와 사망자에 대해 기록한 기존 문서는 단순한 표 형태로 사망자와 부상자의 수치만 보여주었습니다. 나이팅게일은 사망 원인에 대한 강렬한 인상을 심어주기 위해
-
학습 길잡이 기타
숫자 대할 때 1이 자주 나타나는 이유는 뭘까요?
우리가 일상에서 만나는 숫자들을 떠올려봅시다. 인구수, 전기 사용량, 회사 매출액, 심지어 강의 길이까지. 이런 데이터들을 무작위로 모아놓으면, 1부터 9까지의 숫자가 첫 자리에 고르게 분포할 거라고 생각하기 쉽습니다. 그래서 만약 사람이 적당히 창작해서 만들어 넣으면 보통 처음 시작하는 수가 심하게 치우치지 않고 적당히 분산되어 있습니다. 하지만 놀랍게도 현실은 전혀 그렇지 않습니다. 자연스럽게 생성되고 측정된 수치들은 첫 자리가 1로 시작하는 경우가 압도적으로 많고, 그 뒤로 갈수록 줄어듭니다. 이 현상을 ‘벤포드 법칙’이라고 부릅니다.이러한 경향은 AI의 도움을 받는다면 어렵지 않게 확인해볼 수 있습니다. 대중적인 AI 도구를 사용해 대륙별로 대표적인 국가 47개국의 인구 정보를 모아보았는데요, 그중 30%가량은 1로 시작합니다. 2로 시작하는 경우는 13% 정도네요. 7, 8, 9로 시작하는 경우는 겨우 5% 남짓에 불과합니다. 잠깐이면 되니 여러분도 시간을 내어 한번 해보기를 권합니다.마치 자연은 1이라는 숫자를 특히 사랑하는 듯합니다. ‘자연스러운’ 수들은 각자가 나타날 확률이 n분의 1쯤 될 것 같지만, 우리의 직관과 달리 “작은 숫자가 첫 자리에 나타날 가능성이 훨씬 높다”는 이 불균형한 분포는 조금이라도 관심을 기울여본 사람들에게 신비로운 느낌을 줍니다.이 이야기는 사실 19세기 말 한 천문학자의 호기심에서 시작됩니다. 캐나다 출신 천문학자 사이먼 뉴컴은 도서관에서 자주 쓰이는 로그표 책을 관찰하다 이상한 점을 발견했습니다. 책의 앞부분, 즉 1로 시작하는 구간은 손때가 많이 묻어 낡았지만, 9로 시작하는 뒷부분은 거의 새 책처럼 깨
-
학습 길잡이 기타
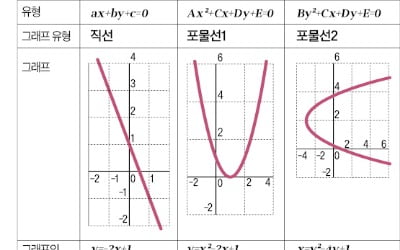
2차 관계식은 도형의 완벽함 그려내는 마법 주문
Ax2 + By2 + Cx + Dy + E= 0라는 복잡한 식을 보면 머리가 지끈지끈 아파올 수도 있습니다. 하지만 이 식 속에 눈에 보이지 않는 아름다운 도형의 세계가 숨어 있다면 믿으시겠습니까? 일차식인 이 좌표평면 위에 단순하고 명확한 직선을 그려내듯, 이 딱딱한 이차 관계식 또한 단순한 계산식이 아닙니다. 이 식은 곧 좌표평면 위에 도형의 완벽함과 우아함을 그려내는 마법의 주문입니다. 이제 그 신비로운 변신 과정을 함께 확인해보시죠.자, 이제 미지수가 x, y 2개인 이차방정식의 일반형을 떠올려봅시다.Ax2 + By2 + Cx + Dy + E= 0이 복잡한 식을 그래프로 나타낼 수 있을까요? 물론입니다. 오늘은 이차 관계식에 대해 생각해보려고 합니다. 우리가 이차 관계식을 이야기할 때, 적어도 x2이나 y2항은 하나라도 있어야 의미가 있습니다. 먼저 A는 0이 아니고 B가 0인 경우를 생각해보겠습니다. 이때 방정식은 Ax2 + By2 + Cx + Dy + E= 0의 형태가 됩니다. 이 식을 y에 대해 정리하면 다음과 같이 됩니다(단, D=0이라고 가정합니다).Dy=−Ax2−Cx−E 양변을 D로 나누어 정리하면,이는 결국 우리가 익히 아는 y=ax2 + bx +c 꼴의 이차함수로 귀결됩니다. 이 함수를 좌표평면 위에 그리면 바로 포물선이 됩니다. 중학교 3학년 과정에서 배우는 것처럼, 이차항의 계수의 부호에 따라 그래프의 모양이 결정됩니다. 계수가 양수면 아래로 볼록한 포물선이, 음수면 위로 볼록한 포물선이 그려지게 됩니다. 이처럼 복잡해 보이던 이차 관계식의 특정 조건이 곧 우리에게 익숙한 포물선을 그려내는 셈입니다. 그렇다면 이번에는 A=0이고 B가 0이 아닌 경우를 생각해봅시다. 이때 방정식은 By2+Cx+Dy+E=0의 형태가 됩니다.이 식을 x에 대해 정리하면, ‘