전체뉴스
-
경제 기타
EU 정상회의 '해피엔딩'…유로존 위기 급한불 꺼지나
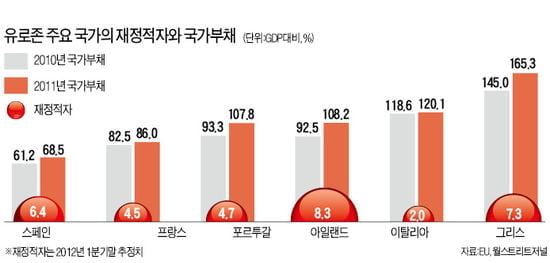
“이제껏 열린 EU 정상회의 중 가장 성공적이다.”(월스트리트저널) 지난달 28, 29일 열린 유럽연합(EU) 정상회의는 일단 '해피엔딩'으로 끝났다. 독일은 예상을 깨고 유럽기금으로 재정위기국 국채를 직접 매입하라는 이탈리아와 스페인의 요구사항을 전격 수용했다. 하지만 합의 내용을 실행에 옮기기까지 정치적·법적 장애물이 만만치 않아 효과가 단기에 그칠 것이란 비관론도 고개를 들고 있다. 독일 내 반발도 거세지고 있다. #예상외의 결과…시장...
-
경제 기타
(70) 베블렌 효과는 불안 때문에 나타나는 것일까?
공황장애는 특별한 이유 없이 예상치 못하게 나타나는 극단적인 불안 증상을 말한다. 국민건강보험공단에 따르면 2006년 3만5195명이던 공황장애 환자가 5년이 지난 2011년 5만8551명으로 68.5% 증가했다. 인구 1천명당 1.2명이 공황장애를 앓고 있는 셈이다. 그만큼 현대인은 불안 속에서 살고 있다. 《불안》의 저자 알랭 드 보통(Alain de Botton)에 따르면 인간이란 지위에서 불안을 느낀다. 그리고 지위에 대한 갈망이 지나...
-
경제 기타
'빠르고 안전한' DHL… ', 세계를 누비는 물류 거인' 페덱스
DHL - 페덱스 '옐로(yellow) 또는 화이트(white).' 물품을 가장 빠르게 외국으로 보내고 싶다면 노란색과 흰색 비행기 중 하나를 골라야 한다. 하늘길을 놓고 쟁투를 하는 영원한 맞수 DHL과 페덱스다. DHL은 물류 전체 부문 세계 1위 기업이다. 물동량을 기준으로 다른 기업을 압도한다. 페덱스는 '항공 특송'의 대명사다. 세계 시장 점유율은 3위지만 미국 시장만 놓고 보면 단연 1위다. DHL과 페덱스의 세계 항공특송 시장 ...
-
경제 기타
인천공항 민영화 해야할까요
찬 "시설 투자재원 마련·경쟁력 강화위해 필요" 반 "해마다 막대한 이익 내는데 왜 매각하나" 인천공항 민영화가 뜨거운 이슈로 떠올랐다. 특히 연말 대선을 앞두고 민영화를 연내 끝내야 하는 것인지 아니면 이를 차기 정권으로 넘겨야 하는지, 정치권 안팎에서 치열한 갑론을박이 계속되고 있다. 이 문제는 당초 정부가 추진했지만 정치권의 반대로 무산됐다가 정부가 이를 재추진하면서 19대 국회에서 관련법이 처리될 수 있을지 주목되는 상황이다. 정...
-
TESAT 공부하기 기타
"졸업 전까지 TESAT 자격증 꼭 따라"
동국대·인제대도 졸업시험으로 테샛 도입…한경과 MOU 맺은 '테샛클럽' 10개大로 동국대와 인제대가 잇따라 '한경 테샛 대학클럽'에 합류했다. 테샛클럽이란 상경계 학생들이 졸업 전까지 국가공인 경제이해력 검증시험인 테샛(TESAT) 자격증을 따 제출하면 졸업시험을 통과한 것으로 인정하는 대학들의 모임이다. 테샛클럽에는 현재 두 대학을 비롯해 한국외국어대, 한림대, 강원대, 방송통신대, 창원대 등 10개 대학이 합류한 상태이며 3개 대학이 추...
-
학습 길잡이 기타
최문섭의 신나는 수학여행-박희성의 맛깔난 잉글리시
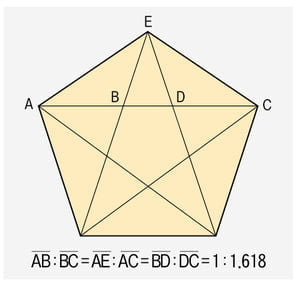
최문섭의 신나는 수학여행 - 담배의 길이는 누가 정했을까? 신용카드, 은행통장, 명함, 노트북, 락앤락 통, 방안의 스위치박스, 벽의 콘센트, 스마트폰, 담뱃갑, 성냥,… 이들의 공통점은 대체 무엇일까? 아마 눈치가 빠른 사람이라도 이들의 공통점을 단번에 찾기란 쉽지 않을 것이다. 나조차도 이 글을 쓰기 전엔 몰랐었으니까! 사실 위에 언급한 것들은 '황금비'라는 수학적 비를 이용해 디자인 된 제품들이다. 황금비! 아마 TV를 통해서든 책자를...
-
학습 길잡이 기타
Smart한 논술의 법칙 (23) 문제에 현혹되지 말고 기본으로 돌아가라!
▧ 들어가며… 안녕하세요. 많은 학교에서 기말고사를 앞두고 있거나 기말고사를 보고 있을 것입니다. 준비한 대로 공부한 만큼 시험 잘 보기 바랍니다. 이번주에 이어 살펴볼 논술 문제는 광운대입니다. 광운대의 논술경향과 특징은 작년에 제가 연재한 논술 프로파일링에 잘 정리돼 있으니 참고하면 좋을 것입니다. 광운대 논술은 2시간 동안 1400자 내외를 써야 하는 시험이며, 올해 4개 영역 중 2개 영역 3등급 이내라는 수능최저등급이 신설됐습니다...
-
학습 길잡이 기타
변증법 (2)
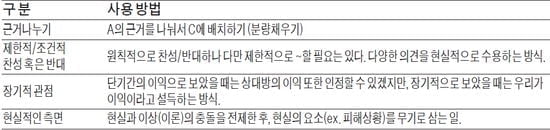
오늘은 지난 시간에 이어서 변증법에 대한 이론을 알아보고, 그 실례로 해답을 어떻게 꾸리는지 알아보도록 하겠습니다. ▨C를 만드는 방법 몇 가지 지난 시간에 C를 만드는 꼼수 몇 가지, <근거나누기><제한적/조건적 찬성-반대><장기적인 관점>에 대해서 알아보았지요. 오늘은 마지막으로 <비현실적 관점>(=현실적인 측면)을 설명드리지요. 그렇게 어려운 것은 아닙니다. 상대방의 관점을 인정하면서도 그 ...