-
학습 길잡이 기타
π 적극적으로 사용한 오일러, 대중화 이끌었죠
오늘은 수학에서 빼놓을 수 없는 아주 특별한 기호 π(파이)에 관해 이야기해보려 합니다. 우리가 지금은 아무렇지 않게 사용하는 이 기호를, 다시 생각해보면 ‘왜 이렇게 쓰게 되었지?’ 하고 새삼 궁금할 때가 있습니다.π를 처음 배우는 건 초등학교에서지만, 기호로서 π를 배우는 것은 중학교 1학년 때입니다. ‘원의 둘레와 지름의 비율’이라고 간단히 배우지만, 사실 옛날에는 이를 표현하는 방법이 제각각이었습니다. 고대 그리스에서는 따로 기호 없이 “원의 둘레는 지름의 약 22/7배쯤 된다”고 설명했고, 중세 유럽에서는 “proportio circumferentiae ad diametrum”처럼 라틴어 문장으로 길게 표현했습니다. 17세기에는 c(둘레, circumference)와 d(지름, diameter)를 사용해 c/d처럼 직접 분수 형태로 나타내는 방식도 있었지요.이런 혼란을 정리한 사람이 바로 1706년, 영국의 수학자 윌리엄 존스(William Jones)입니다. 그는 라는 책에서 처음으로 π를 원주율을 나타내는 기호로 사용했습니다. 왜 하필 π였을까요? π는 그리스어 ‘periphery(둘레)’의 첫 글자이기 때문입니다. ‘원의 둘레’와 관련된 비율이니, 둘레를 의미하는 단어의 첫 글자를 따온 것이지요.하지만 당시에는 π가 금방 대중화되지 않았습니다. π를 전 세계 수학자에게 널리 퍼뜨린 인물은 바로 수학의 거장 레온하르트 오일러(Leonhard Euler)입니다. 오일러는 특히 자신의 논문과 저술에서 원주율을 간결하고 일관되게 표현하기 위해 π를 적극적으로 사용했습니다. 대표적으로 오일러는 삼각함수와 원주율을 연결 지은 공식, 예를 들어 오일러 공식인 같은 식을 통해 π를 자연스럽게 수학의 중심 개념으로
-
신동열의 고사성어 읽기
三旬九食 (삼순구식)
▶한자풀이三: 석 삼 旬: 열흘 순 九: 아홉 구 食: 먹을 식한 달에 아홉 끼를 먹다몹시 가난함을 이르는 말- <후한서>삼순구식삼순구식(三旬九食)은 ‘열흘에 아홉 끼를 먹다’라는 뜻으로, 매우 가난함을 이르는 말이다. 남북조시대 송나라의 범엽이 후한의 역사를 정리한 <후한서>에 나오는 표현이다. 후한 시대 가난한 백성들의 삶을 묘사하면서 이 말이 사용되었다. 삼순(三旬)은 한 달을 의미하며, 구식(九食)은 아홉 끼니를 뜻한다. 즉 한 달 동안 겨우 아홉 끼니를 먹을 정도로 극심한 가난을 겪는 상황을 나타내는 말이니, 당시 백성들이 얼마나 어려운 삶을 살았는지를 생생하게 묘사한 사자성어다.송나라를 대표하는 도연명 시인의 시에도 삼순구식이 나온다. 그는 잠시 현령이라는 관직에 있었지만 “다섯 말의 쌀 때문에 부패한 관리들에게 허리를 굽힐 수 없다”라는 말을 남기고 낙향해 많은 작품을 남겼다. 그의 시 중에는 이런 구절이 있다.“동방에 한 선비가 있으니, 옷차림이 항상 남루했고, 한 달에 아홉 끼가 고작이요(三旬九食) 10년이 지나도록 관직 하나로 지내더라. 고생은 비할 데가 없건만 늘 밝은 얼굴이더라. 내 그분을 뵙고자 이른 아침에 갔더니, 푸른 소나무는 길옆에 울창하고, 흰 구름은 처마 끝에 잠들었더라.”자신의 처지를 동방의 한 선비에 비유한 시로 읽힌다.상루하습(上漏下濕)은 ‘위에서는 비가 새고 아래에서는 습기가 차오른다’라는 뜻으로, 몹시 가난한 집을 이르는 말이다. 위로는 비가 새고 옆으로는 바람이 들이친다는 상우방풍(上雨旁風), 집이 네 벽뿐이라는 가도사벽(家道四壁)도 집안 형편이 매우 어려움을 뜻하는
-
대입 전략
"차라리 문과로 바꿔 한단계 위 대학 가자"…학습부담 큰 이과 중위권, 문과 전향 급증
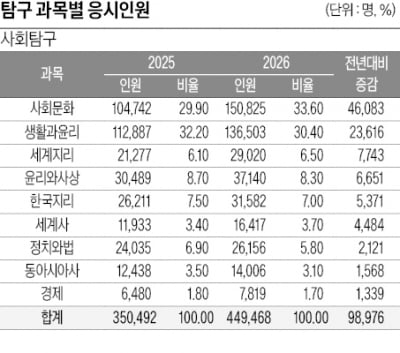
고3 3월 학력평가는 현 수능 체제와 유사한 첫 전국 모의고사다. 당해 연도 대입 수험생의 성향 및 특성 등을 파악하기에 좋다. 국어, 수학 선택과목 응시 비율, 사탐과 과탐 응시 비율 등을 통해 문과생, 이과생의 흐름을 분석할 수 있어 대입 전략을 수립하는 데 가장 기초적인 판단 기준이라고 할 수 있다.특히 국어와 수학 선택과목에 따른 유불리가 극심한 현 수능 체제에서 수험생들은 다양한 변수를 고려하고, 1년간의 수능 학습의 밑그림을 촘촘하게 세워둬야 한다. 필요하다면 선택과목을 변경하는 결정을 내려야 할 수도 있다. 경쟁 관계인 수험생 집단의 과목 선택 및 지원 성향을 파악해두면 6월, 9월 모의평가를 거치며 선택과목 변경 여부 등을 판단하는 데 큰 도움을 얻을 수 있다.종로학원이 3월 학력평가 응시 현황을 분석한 결과, 2026학년도 대입 고3 수험생 사이 문과 학생이 증가한 것으로 분석됐다. 최근 몇 년간 이과 선호, 의대 열풍 등의 상황과 비교해보면 이례적인 변화라 할 수 있다.구체적으로, 3월 학력평가 기준으로 수학 과목에서 이과생이 주로 응시하는 미적분, 기하 응시 비율은 지난해 46.1%에서 올해 40.5%로 5.6%포인트 하락했다. 미적분, 기하 응시 비율은 2022학년도 통합 수능이 도입된 이래 꾸준히 증가해왔다. 응시 비율은 2022학년도 39.5%, 2023학년도 43.2%, 2024학년도 46.1%, 2025학년도 46.1%로 최고치를 기록했다. 2026학년도 40.5%로 크게 하락했다. 반면 문과 학생들이 주로 응시하는 확률과통계는 지난해 53.9%에서 올해 59.5%로 5.6%포인트 상승했다.국어 과목에서는 이과생이 많이 응시하는 언어와 매체 선택 비율이 지난해 37.4%에서 올해 33.8%로 3.6%포인트 하락했다.수학에서 미적분, 기하
-
영어 이야기
돌파구, 획기적인 발전 'breakthrough'
Samsung Heavy Industries, a major Korean shipbuilder, has made a breakthrough in its liquefaction technology for floating liquefied natural gas (FLNG) production facilities, challenging long-standing dominance by US rivals.The technology, known as SENSE IV, is often referred to as the “heart” of the FLNG unit, a massive offshore structure that extracts, liquefies and transfers natural gas from subsea fields. FLNG construction usually costs between 2 trillion won and 4 trillion won per unit, with liquefaction equipment accounting for as much as 35% of that figure.Despite Korea’s dominance in shipbuilding, critical components such as LNG liquefaction systems have long been supplied by US and European firms, including North Carolina-based engineering firm Honeywell International.With SENSE IV, Samsung Heavy is aiming to break that reliance.삼성중공업은 부유식 액화천연가스(FLNG) 생산 설비용 액화 기술 분야에서 획기적인 성과를 거두며 오랫동안 이 분야를 장악해온 미국 경쟁사들에 도전장을 내밀었다.SENSE IV로 알려진 이 기술은 FLNG 설비의 ‘심장’으로 불리며 해저 가스전에서 천연가스를 추출해 액화한 뒤 이를 육상으로 이송하는 거대한 해상 구조물의 핵심 장비다. FLNG 설비 건조에는 통상 한 기당 2조 원에서 4조 원 비용이 들며, 이 중 액화 장비가 최대 35%를 차지한다.한국은 조선 분야에서 세계적인 경쟁력을 확보하고 있지만 그동안 LNG 액화 시스템과 같은 핵심 부품은 미국과 유럽 기업, 특히 노스캐롤라이나에 본사를 둔 허니웰 인터내셔널 등에 의존해왔다.삼성중공업은 SENSE IV 기술을 통해 이러한 의존도를 줄일 계획이다. 해설 우리나라는 세계 1위의 조선 강국입니다. HD현대, 한화오션, 삼성중공업 등 세계적인 조선 회사들이 있지요. 원유, 석유제품 등을 운반하는
-
대학 생글이 통신
스트레스 극복하려면 나만의 휴식 찾기를
저는 원하는 대학에 들어가기 위해 1년 동안 입시를 다시 준비했습니다. 그 시간 동안 저에게 힘이 되어준 취미 활동에 대해 이야기해보려고 합니다.대학수학능력시험을 다시 준비하면서 공부 외 취미 생활과 관련해 두 가지 원칙을 세웠습니다. 첫 번째는 일주일에 하루는 ‘편안한 날’로 정하기였습니다. 하루 10시간씩 공부하는 일상을 쉬는 날 없이 지속하기는 어려웠습니다. 일주일에 하루 정도는 휴식일을 가지라는 부모님의 권유도 있었습니다.그래서 저는 일요일을 편안한 날로 정했습니다. 일요일엔 늦잠을 자기도 하고, 좋아하는 카페에 가서 그림을 그리거나 친구들과 만나 점심을 먹으며 대화를 나누기도 했어요. 아무것도 하기 싫은 날엔 도서관에 가거나 놀이터에 가서 멍하니 앉아 있기도 했고요. 여기서 중요한 것은 단지 공부를 안 하고 마음껏 노는 것이 아니라 무엇을 하든 내가 쉬고 있다고 느끼는 것입니다.두 번째 원칙은 학업과 취미를 확실히 분리하기였습니다. 저는 음악 듣는 것을 좋아했지만, 재수를 시작하면서 공부하는 시간에는 음악을 완전히 끊었습니다. 수능 시험장에서는 음악을 들을 수 없으니 음악과 멀어지자고 다짐한 것이었죠. 그 대신 그날그날 공부를 끝내고 나면 집으로 돌아가는 길에 좋아하는 노래를 들으며 저 자신에게 작은 보상을 주었습니다.혼난 뒤에 먹는 사탕이 더 달콤하다는 말을 들어보셨나요? 저에게는 하루종일 공부하고 집에 돌아가며 음악을 듣는 시간이 수험 생활을 버틸 수 있게 하는 사탕과 같은 역할을 했습니다. 수능이 코앞으로 다가오면서부터는 음악 듣는 시간을 더 줄였지만, 수험생 시절을 떠올려보면 그 시간의 기억이 가장 선명
-
최준원의 수리 논술 강의노트
도형 활용 미적분 자주 출제돼…증명 연습도 필요
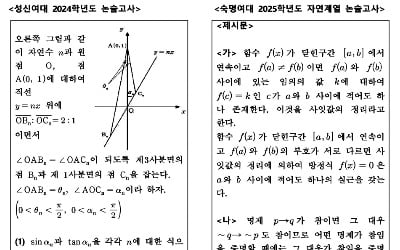
이들 대학은 모두 미적분 중심의 문항을 출제하며 시험시간과 문항 수, 출제 유형 및 난이도에서도 매우 유사하다는 공통점이 있다. 특히 기본 도형에 기초한 미적분 문항이 주로 출제되므로 도형을 활용해 미적분 문제 해결력을 높이는 것이 합격의 관건이라고 할 수 있다. 또 수학적귀납법이나 사잇값 정리에 대한 간단한 형태의 증명 문제도 간헐적으로 출제되므로 교과서의 증명 예제를 여러 번 반복해서 확실하게 익혀두어야 한다. ◆ 숙명·성신·동덕여대◆ 수리논술 대비 포인트 1. 기본도형에 기반한 미적분 문제해결력을 요구하는 문항이 주로 출제됨.- 수열, 삼각함수의 공식 등을 자주 활용하므로 이를 숙지해야 함.2. 수학적귀납법, 사이값정리에 대한 간단한 증명 문제가 출제되므로 교과서의 증명 예제를 확실하게 익혀두어야 함.
-
대학 생글이 통신
게임·애니…영상학과서 콘텐츠 도전하세요
저는 중학생 때 우연한 계기로 영상에 관심을 갖게 되었습니다. 이후 고등학교에서도 영상과 관련한 활동을 많이 했습니다. 영상에 대한 관심과 열정이 저를 영상학 전공으로 이끌었습니다. 오늘은 제가 다니고 있는 성균관대 영상학과에 대해 소개해보려고 합니다.성균관대에는 콘텐츠를 다루는 학과가 여러 곳 있습니다. 인문·사회 계열의 미디어커뮤니케이션학과와 컬처앤테크놀로지융합전공, 예술대학의 영상학과가 대표적입니다. 이들 전공은 콘텐츠를 다룬다는 점에서 비슷하지만, 접근 방식은 다릅니다. 그중 영상학과는 예술로서의 영상, 즉 스토리 중심의 영상 콘텐츠 제작을 배우는 학과입니다.영상학과에서는 영화를 비롯한 영상을 하나의 학문으로 바라봅니다. 게임, 애니메이션, 영화, 영상이론, 미학 등 다양한 세부 분야를 전공한 교수들이 연구하고 학생들을 지도합니다. 학과 복도에 붙어 있는 교수들의 추천 영화 포스터만 보더라도 영상학과가 무엇을 배우는 곳인지 알 수 있습니다.영상학과 1학년은 ‘촬영 기초’라는 전공 필수 수업을 수강합니다. 이 수업에선 단편영화를 제작하는 데 필요한 기초적인 내용을 배웁니다. 팀을 이뤄 카메라를 들고 나가 촬영하고, 학생들이 직접 연출하고, 촬영한 영상을 편집해 작품을 완성합니다. 쉽지 않은 과정이지만, 예술로서 영상을 이해하고 스토리의 본질에 대해 탐구할 수 있는 좋은 기회입니다.영상학과 학생들은 4학년이 되면 졸업 작품을 준비합니다. 영화, 애니메이션, 모션그래픽, 인터랙티브 아트, 게임까지 다양한 영상매체 중 하나를 선택해 자기만의 작품을 만들어내는 것입니다. 수많은 장르가 있지만 영상학과에서 다루
-
홍성호 기자의 열려라 우리말
'폭싹 속았수다'에 담긴 또 다른 문법들
넷플릭스의 화제작 ‘폭싹 속았수다’는 그 인기 못지않게 우리말 적는 방식에 대한 주목도도 함께 높였다. 지난 호에서 살펴본 ‘폭삭’과 ‘폭싹’의 관계는 한글맞춤법 가운데 ‘소리 적기’ 방식에 관한 이해가 필요하다. 이에 따르면, ‘ㄱ, ㄷ’ 같은 폐쇄음 받침 뒤에서는 자음이 자연스럽게 된소리로 나므로 굳이 이를 표기에 반영하지 않는다고 했다. ‘깍뚜기’가 아니라 ‘깍두기’, ‘덥썩’이 아니라 ‘덥석’으로 적는 게 그런 까닭이다. ‘쌕쌔기→쌕쌕이, 오뚜기→오뚝이’로 바꿔하지만 겹쳐 나는 소리에서는 이와 상관없이 같은 글자로 적는다. ‘쌕쌕거리다, 짭짤하다’(쌕색- ×, 짭잘- ×) 같은 게 그 예이다(한글맞춤법 제13항). 그러면 ‘쌕쌕거리다’에서 접미사 ‘-이’가 붙어 파생된 말은 ‘쌕쌕이’일까 ‘쌕쌔기’일까? 이를 구별하기 위해서는 한글맞춤법을 여는 두 가지 열쇠 중 나머지 ‘형태 밝혀 적기’에 관한 규칙을 알아봐야 한다.우리 맞춤법에 “‘-하다’나 ‘-거리다’가 붙는 어근에 접미사 ‘-이’가 붙어서 명사가 된 것은 그 원형을 밝히어 적는다”는 규정이 있다(한글맞춤법 제23항). 이는 접미사가 붙어서 새로 만들어진 말의 발음이 달라질 때 원래 형태를 어떻게 적을 것인가를 규정한 것이다. 가령 ‘쌕쌕거리다, 오뚝하다’의 어근인 ‘쌕쌕’ ‘오뚝’에 접미사 ‘-이’가 결합해 새말을 만든다. 그것을 그동안은 ‘쌕쌔기’ ‘오뚜기’라고 적었다. 우리말 표기의 근간 중 하나인 &lsq