#생글생글
-
대입전략
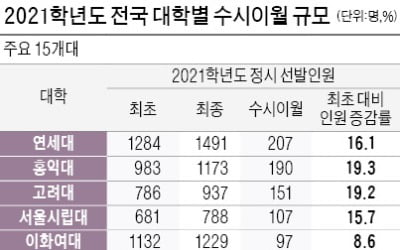
연세대·고려대 계획보다 정시인원 더 뽑아…약대 중복합격으로 이탈자 더 늘어날 듯
지난해 전국 대학의 수시이월 인원은 총 4만1382명에 달했다. 정시에서 뽑기로 했던 최초 계획과 비교해 실제 정시에선 4만 명 넘는 인원을 더 선발했다는 것이다. 수시이월 규모가 정시 지원전략에서 가장 중요한 요소 중 하나인 이유다. 올해 고3 학생 수는 전년과 비교해 비슷한 수준이다. 수시이월 규모 또한 비슷할 것으로 전망된다. 2021학년도 전국 대학별 수시이월 규모를 분석해본다. 수시이월은 수시에서 뽑지 못해 정시로 이월해 선발하는 인...
-
생글기자
유기견 안락사보다 보호수용 해법 찾아야
반려견을 기르는 가정이 늘면서 유기견도 늘고 있다. 동시에 떠오르고 있는 문제가 유기견 안락사다. 유기견 안락사에 대해 찬반 의견을 정하기는 쉽지 않다. 유기견 안락사는 어느 정도 불가피한 면이 있다. 유기견을 보호하려면 시설이 필요하고 비용도 들어간다. 모든 유기견을 수용할 수 있는 시설이 있다면 굳이 안락사시킬 필요는 없겠지만 현실은 그렇지 않다. 위생 문제도 따른다. 병이 들어 고통스럽게 살아가는 유기견도 있다. 회복할 가능성이 없는 ...
-
주코노미의 주식이야기
배당은 기업이 번 돈의 일부 주주에게 나눠주는 것
주식과 배당주식시장의 오랜 격언 중에 ‘찬바람이 불면 배당주에 투자하라’는 말이 있습니다. 연말이 다가오면 배당주를 매수하라는 소리죠. 배당주가 무엇이길래 겨울에 배당주를 사라고 하는 것일까요? 오늘은 기업의 배당에 대해 알아보겠습니다. 주식에 투자해서 수익을 얻는 경우를 생각해볼까요? 가장 먼저 떠오르는 것은 주가가 올라서 생긴 이득일 것입니다. 시세차익이라고도 하죠. 1만원에 산 주식이 1만2000원으로 올랐다면 내 ...
-
대학 생글이 통신
시험·면접 스트레스 '데미지 컨트롤'로 이겨내볼까
큰 시험 또는 중요 면접 준비에 두어 주 정도밖에 남지 않은 것 등을 위기 상황으로 느끼는 경우가 많습니다. 날짜가 가까워질수록 조급한 마음에 이것도 하고, 저것도 하고, 끝내는 모든 것이 부족한 느낌이 들어 불편한 생각이 많아지곤 합니다. 이런 때 여러분이 알았으면 좋겠다 싶은 것은 바로 ‘데미지 컨트롤’ 기술입니다. 어려운 상황이 올 때, 마음이 힘들고 스트레스가 올 때, 성적이 아무 이유 없이 떨어질 때, 어떤 방법으...
-
대학 생글이 통신
수험 생활 끝낸 지금…색다른 경험 해보면 어떨까요
수능이 끝난 지금 수험생 여러분은 무엇을 하고 계시나요? 대부분 무언가를 하기보다는, 무엇을 해야 할지 생각하며 시간을 보낼 거라 예상합니다. 마음속 한편에 갖고 있는 고민에 대한 답을 찾을 수 있게 제 경험을 전해드립니다. 수시 원서를 쓴 수험생들이라면 수능을 마친 뒤 생각보다 할 일이 많을 것입니다. 수능 준비하느라 다소 미뤄 놓았던 대학별고사를 준비해야 합니다. 대학마다 시험 종류, 일정이 다 다르기에 이에 맞춰 그동안 준비했던 모든 것...
-
커버스토리
수능 국어·논술 출제유형에 대비해볼까
한국경제신문 기사 읽어보기 물가·집값 폭등으로 지갑 두께가 얇아지자 ① 근로자들의 임금 인상 요구가 빈번해지고 있다. 기업들이 중장기적으로 불어나는 ② 인건비를 제품 가격에 전가 하거나 고용을 줄일 우려도 커지고 있다. 고용노동부에 따르면 상용근로자의 올해 3분기(7~9월) 월평균 임금 증가율(5.0%)은 분기 기준으로 2018년 1분기(7.9%) 후 가장 높았다. ③ 임금이 뛰는 것은 치솟는 물가와 관계가 깊다. 한...
-
임재관의 인문 논술 강의노트
중앙대 2번 공통유형…반복적 기출풀이 필수
마 동남아인 두 여인이 소곤거렸다 고향 가는 열차에서 나는 말소리에 귀 기울였다 …(중략)… 두 여인이 잠잠하기에 내가 슬쩍 곁눈질하니 머리 기대고 졸다가 언뜻 잠꼬대하는데 여전히 알아들을 수 없는 외국말이었다 …(중략)… 한잠 자고 난 아기 둘이 칭얼거리자 두 여인이 깨어나 등 토닥거리며 달래었다 한국말로, 울지 말거레이 집에 다 와 간데이 라 “내선일체...
-
숫자로 읽는 세상
美 실리콘밸리 인구의 6%에 불과한 인도계…MS·알파벳 등 IT업계 CEO 차지한 비결은
마이크로소프트(MS) IBM 알파벳 트위터. 미국의 대표 정보기술(IT) 업체인 이들 기업의 최고경영자(CEO)는 모두 인도계다. 지난달 말 퍼라그 아그라왈이 37세에 트위터 CEO로 임명되면서 미 S&P500 기업의 최연소 CEO 자리도 인도계 차지가 됐다. 글로벌 CEO를 다수 배출한 인도는 다양한 지형과 인종, 문화가 어우러진 나라다. 인도인들이 태어날 때부터 조화와 협력을 배우며 자연스럽게 경영 기술을 체득하는 배경이다. 온화하...