생글 학습·진로 기타
-
대입전략
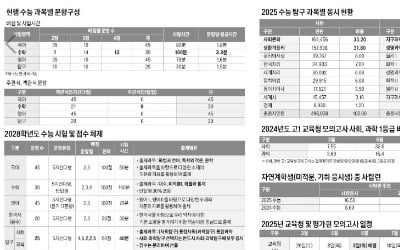
통합과학 영향력 커지고 심화 수학 출제 제외…사탐·과탐 문항 늘고 배점은 3단계로 세분화
올해 고1이 되는 학생부터 적용되는 2028학년도 대입 수능에서는 탐구과목 영향력이 상당히 높아질 것으로 보인다. 현재 탐구과목은 사탐 9과목, 과탐 8과목 중 두 과목을 선택하는 방식이고, 수험생 입장에서 가장 부담이 덜한 과목에 집중적으로 응시하고 있다. 사탐 9과목 중에서는 2025학년도 수능 기준으로 사회문화 33.2%, 생활과 윤리 31.8%로 이 두 과목에 65.0%가 집중됐다. 과탐에서는 8과목 중 지구과학1 36.0%, 생명과학1 32.7%로 두 과목에 집중된 상황이다.2028학년도부터 수험생은 통합사회·통합과학 두 과목에 모두 응시해야 한다. 시험시간 또한 현재 한 과목당 30분이지만, 2028학년도부터는 40분으로 늘어나고 문항 수도 기존 과목당 20문항에서 25문항으로 늘어난다. 수험생 입장에서는 문항 수와 시간이 늘어난 것 자체가 부담일 수 있다.사회·과학에서 두 과목만 선택하는 현재 수능 구도에서 탐구 시험 영역 자체가 17개 영역으로 늘어나고, 문항 수도 늘어난다. 시험 영역 간 통합으로 출제되기 때문이다. 또한 탐구영역의 문항별 배점이 현재 2점, 3점 이원화에서 1.5점, 2점, 2.5점으로 삼원화 체제로 바뀐다. 배점 문항이 세분되어 변별력이 더 높아질 수 있다. 탐구영역은 전반적으로 시험 영역도 확대되었고, 여기에 따라 문항 수, 시험시간, 배점 체제가 모두 늘어나 현재보다 변별력은 더 커질 것으로 보인다.수능 과목 탐구영역은 통합사회·통합과학에서 50문항으로 국어, 수학, 영어보다 많다. 현재까지는 국어 45문항, 영어 45문항, 수학 30문항, 탐구 두 과목 40문항(각 20문항)으로 국어, 영어 문항 수가 가장 많지만 2028학년도부터는 탐구 문항 수가 가장 많게 된다.배점도 현재 국어·
-
영어 이야기
외관상의 작은 변화를 말할 땐 'nip and tuck'
The IONIQ 5 will greet drivers this month with its retouched looks and enhanced functions. It got its first nip and tuck for the first time since its launch three years ago.Powered by a fourth-generation battery with a bigger 84.0 kilowatt hours (kWh) capacity, the new crossover EV sport utility vehicle (SUV) can drive 485 kilometers on a single charge, versus 458km on its previous version electrified by a 77.4-kWh battery.With a 350kWh super-fast charger, its battery can be charged by 80% in 18 minutes, Hyundai Motor said.Along with the performance improvements, its drivers will enjoy enhanced safety features such as a hands-on detection (HOD) steering wheel, lane keeping assist 2, remote smart parking assist 2 (RSPA 2) and forward/side/reverse parking collision-avoidance assist (PCA-F/S/R).아이오닉 5는 이번 달 새로워진 디자인과 향상된 기능으로 운전자들을 맞이할 준비를 마쳤다. 출시 3년 만에 외양과 기능에 변화를 준 것이다.4세대 배터리를 탑재한 새로운 크로스오버 전기차 SUV인 아이오닉 5는 배터리 용량을 기존 77.4킬로와트시(kWh)에서 84.0kWh로 확장해 1회 충전 주행 가능 거리가 458km에서 485km로 늘어났다.또 350kWh급 초급속 충전 시 18분 이내 배터리 용량의 80%까지 채울 수 있다고 현대자동차는 밝혔다.이러한 성능 향상과 더불어 운전자는 직접식 감지(HOD) 스티어링 휠, 차로 유지 보조 2, 원격 스마트 주차 보조 2(RSPA 2), 전방·측면·후방 주차 충돌 방지 보조(PCA-F/S/R) 등의 안전 기능을 누릴 수 있다.해설전기차는 탄소 배출을 줄이는 친환경 차량으로 주목받고 있습니다. 세계 각국이 기후변화에 대응하기 위해 온실가스 배출 감축을 위한 규제를 강화함에 따라 전기차의 인기는 더욱 높아질 것으로 기대됩니다. 전기차가 더 대중화될 수 있도록 자동차 회사들은 배터리 용량
-
대학 생글이 통신
바뀌는 고교 과정, 선생님께 적극 여쭤보세요
2025학년도부터 고등학교에 새로운 제도가 도입됩니다. 고교학점제가 시행되고, 내신성적 평가 방식이 기존 9등급제에서 5등급제로 바뀝니다. 이런 변화는 대입에도 영향을 미치기 때문에 올해 고등학교에 입학하는 예비 고1은 달라지는 내용을 숙지하고 대비할 필요가 있습니다.고교학점제란 고등학교에서도 대학처럼 학생들이 자기 관심 분야와 진로에 따라 과목을 선택하고 학점을 이수하는 제도입니다. 이때 중요한 것은 전공 적합성입니다. 전공 적합성은 대입 수시전형에서 생활기록부를 평가할 때 핵심 요소입니다. 따라서 대입 희망 전공을 염두에 두고 있다면 고등학교에서부터 그와 관련된 과목을 선택해 수강하는 것이 좋습니다.단, 대학 전공과 관련한 과목을 너무 단순하게 생각하지는 말았으면 좋겠습니다. 예를 들어 의과대학 관련 과목이라면 생명과학, 화학 등이 떠오릅니다. 그러나 의대 진학을 준비하는 학생이라고 해서 인문 계열 과목이 불필요한 것은 아닙니다. 제가 다니는 대전대 한의과대학의 교육 목표를 보면 “인간 존중의 가치관을 바탕으로 윤리의식을 함양한다”는 내용이 있습니다. 단순히 이과 계열 수업만 집중적으로 듣는다고 해서 전공 적합성이 높아진다고 할 수는 없습니다. 대학, 학과마다 요구하는 내용이 다르니 자기가 가고 싶은 대학과 학과의 관련 정보를 확인하는 것이 좋습니다.내신 등급제 변화도 큰 변수가 될 것입니다. 9등급제에서 5등급제가 되면 등급 간 간격이 넓어집니다. 경쟁력을 확보하려면 같은 등급 안에서도 하위 등급보다는 상위 등급에 들어가도록 해야 합니다. 내신 등급의 변별력이 낮아진다면 세부 능력 특기 사항의 중요성이 커질 수
-
홍성호 기자의 열려라 우리말
'제주항공 참사' 대 '무안공항 참사'
#1. 2019년 12월 중국발 외신을 통해 신종 감염병 소식이 국내에 전해졌다. 강력한 전파력이 심상치 않던 이 전염병은 처음엔 ‘우한폐렴’으로 불렸다. ‘우한(武漢)’은 중국 후베이성 성도(省都)로, 이 질병이 처음 발생해 보고된 도시다. 하지만 이 명칭은 오래가지 못했다. 세계보건기구(WHO)에서 곧바로 2020년 2월 공식 명칭을 ‘COVID-19’으로 결정해 발표했기 때문이다. ‘COronaVIrus Disease’를 줄인 말이다. ‘19’는 2019년에 처음 발견됐다는 의미로 붙었다.글쓰기에서 ‘관점’을 잘 살펴야한국 정부 역시 이를 받아 ‘코로나19’로 이름을 바꿨다. 우리 국민에게 ‘코로나’라는 이름이 익숙하다는 점에서 정부가 COVID 대신 그리 정해 부르도록 했다. WHO의 공식 명칭 발표는 새 전염병 이름을 지을 때 특정 지역이나 사람, 동물 이름을 병명에 사용하지 않는다는 원칙에 따른 결정이었다. 해당 지역이나 민족·종교 등에 미칠 부정적 영향, 즉 낙인효과를 막기 위한 노력인 셈이다. 2015년에 도입한 것으로, 이른바 ‘정치적 올바름(political correctness)’의 추구다.#2. 2025년 1월 10일 국토교통부 정례 브리핑에선 다소 이례적인 발표가 있었다. “이번 사고를 두고 일각에서는 ‘무안공항 참사’라고 잘못 표현하고 있습니다. 그릇되게 불리는 것에 대한 지역의 우려가 있습니다.” 그러고는 지난해 12월 전남 무안국제공항에서 발생한 여객기 사고의 공식 명칭은 유가족과 협의한 ‘12·29 제주항공 여객기 참사’라고 다시 한번 확인했다. 이에 앞서 제주도는 올해 1월 초 행정안전부에 사고 명칭을 ‘무안국제공항 제주항공 여객기
-
학습 길잡이 기타
우리 인생에 하나뿐인 제곱수의 해 '2025'
2025년 을사년 뱀띠의 해가 시작된 지 벌써 한 달이 지났습니다. 2025년은 수학과 관련이 많은 수학의 해인 것 같습니다. 2025년이 시작하자마자 SNS와 각종 수학 커뮤니티에서는 2025를 수학으로 이야기하는 글이 많이 올라왔는데, 2회에 걸쳐 이에 대한 이야기를 소개하려고 합니다.2025는 452 = 2025이므로 어떤 정수의 제곱이 되는 정수, 즉 제곱수입니다. 442=1936, 462=2116이니까 어떻게 보면 2025년은 우리의 인생에서 하나밖에 없는 제곱수인 해일 수 있습니다.2025는 신기한 수입니다. 2025를 절반으로 나누어 앞자리 수 20과 뒷자리 수 25를 생각합니다. 20과 25를 더하면 45가 되고, 이 45를 제곱하면 2025가 됩니다. 즉, 2025는 절반으로 나누어 더한 후 제곱하면 원래의 수가 됩니다. 이를 식으로 나타내면 다음과 같습니다.20+25=45, 452=2025여기서 45와 같은 수를 ‘카프리카 수’라고 하는데, 일반적으로 어떤 수의 제곱수를 두 부분으로 나누어 더했을 때 다시 원래의 수가 되는 수를 인도의 수학자 카프리카(D. R. Kaprekar, 1905~1986)의 이름을 붙여 ‘카프리카 수’라고 합니다. 이 카프리카 수에는 다음과 같은 유래가 있습니다.인도의 어느 지역에 있는 철도의 선로 옆에 “3025km”라고 적힌 이정표가 있었습니다. 그런데 어느 날 심한 폭풍우로 인해 이정표가 쓰러지면서 ‘3025’가 ‘30’, ‘25’와 같이 절반으로 나뉘게 되었습니다. 마침 이곳을 지나던 인도의 수학자 카프리카가 30+25=55이고, 552=3025라는 점을 발견했습니다. 그 후 사람들은 55와 같이 어떤 수의 제곱수를 두 부분으로 나누어 더했을 때 다시 원래의 수가 되는 수를 카프리카 수로 부르게 되었습니다.카프리카 수 중에서 두 자리
-
신동열의 고사성어 읽기
割席分坐 (할석분좌)
▶한자풀이割: 벨 할 席: 자리 석 分: 나눌 분 坐: 앉을 좌자리를 잘라서 앉은 곳을 나누다친구과 절교함을 이르는 말 -<세설신어(世說新語)>관영(管寗)과 화흠(華歆)은 중국 한나라 말기에 어려서부터 함께 공부한 친구였는데, 처세나 성품이 서로 매우 달랐다. 관영은 학문을 닦는 데 힘쓰고 부귀영화를 부러워하지 않았으나, 화흠은 언행이 가볍고 부귀영화를 흠모했다.한 번은 두 사람이 함께 채소밭에서 김을 매는 데 땅속에서 금 조각이 나왔다. 관영은 아무 일 없다는 듯 호미질을 계속했지만, 화흠은 그 금 조각을 들고 나가 다 써버렸다. 어느 날은 둘이 함께 글을 읽고 있었는데 집 앞으로 고위 관리의 수레 행렬이 지나갔다. 관영은 전과 다름없이 책을 읽었지만, 화흠은 밖으로 나가 한참을 구경하고 나서야 돌아와 그 행차에 대해 이러쿵저러쿵 떠벌리면서 부러운 기색을 감추지 못했다.관영은 이런 화흠의 태도에 화가 나서 두 사람이 함께 앉아 있던 자리를 칼로 잘라 버리고는 “너는 이제부터 내 친구가 아니다(寗割席分坐曰 子非吾友也)”라고 했다. 나중에 화흠은 오나라 손책의 휘하에 있다가 위나라 조조에게 귀순해 한나라를 찬탈하는 일을 도왔다. 관영은 위나라에서 내린 벼슬을 끝내 고사했다. 이 고사는 <세설신어(世說新語)> 덕행 편에 나오는 이야기다. <세설신어>는 중국 남북조시대 송나라 출신의 유의경이 후한 말부터 동진까지의 문인, 학자, 승려, 부녀자, 제왕 등의 일화를 모아 편찬한 책이다. 이 고사에서 유래한 할석분좌(割席分坐)는 ‘자리를 잘라서 앉은 자리를 나눈다’는 뜻으로 친구와 절교함을 이르는 말이다. 할
-
대학 생글이 통신
3학년 1학기 생기부 포기하지 마세요
올해 고3이 되는 학생들은 지금쯤 어떤 전형을 노려야 할지, 수능에 집중해야 할지, 아니면 학생부종합 전형 준비를 더 해야 할지 고민스러울 것입니다. 저도 수험생 때 비슷한 고민을 했는데요, 그래서 저 같은 ‘수시 최저러(수시전형에서 최저 등급 기준에 맞추기 위해 수능을 공부해야 하는 학생)’ 고3을 위한 조언을 해보려고 합니다.학생부종합 전형과 수능을 모두 잡으려다 보면 두 마리 토끼를 다 놓치게 되지 않을까 생각하는 학생이 더러 있습니다. 그러나 학종은 아직 끝나지 않았습니다. 수시 전형에서는 3학년 1학기까지 학교생활기록부를 평가합니다. 총 5학기 중 5분의 1을 차지하는 한 학기를 포기하는 것은 별로 현명하지 못한 선택입니다. 저도 3학년 1학기 생기부를 포기하지 않았습니다. 오히려 3학년 1학기 생기부에 더 집중해 2학년까지 모자란 성적을 만회했습니다.좋은 생기부를 위해서는 여러 번의 조사와 깊이 있는 고민을 거쳐 탐구 주제를 수집해야 합니다. 매일 뉴스를 세 편 이상 읽고 에세이나 논문도 찾아보면서 비판적 질문을 던지고 의문점을 떠올리는 연습을 해보세요. 이런 질문과 의문점이 곧 탐구 주제가 됩니다.자료 조사를 거듭하다 보면 “우리나라의 환경정책은 어떤 것이 있나”와 같은 질문이 “우리나라의 환경정책의 문제점과 환경 정책이 실효를 거두지 못하는 원인은 무엇인가”와 같은 좀 더 깊이 있는 질문으로 발전합니다. 그러면서 질문에 대한 답도 찾을 수 있게 됩니다.좋은 생기부란 무엇인지에 대해서도 생각해봐야 합니다. 서울대 입학 웹진 아로리 사이트에서는 합격생들의 세부 능력 특기 사항을 볼 수 있습니다. 이 사이트를 참고하
-
영어 이야기
해결하려 애쓰다 'grapple with'
One in five South Koreans is now 65 years old or older as the Asian country grapples with the demographic challenge of a rapidly aging population and the world’s lowest birthrate.The Ministry of the Interior and Safety said that the country has officially joined the super-aged nations, with 20% of its population surpassing the age of 65.South Korea had 10.24 million inhabitants aged 65 and older, accounting for 20% of its total population of 51.22 million.According to the UN, any country with more than 7% of the population 65 or older is an aging society, a country with over 14% of the age group is classified as an aged society and a country with more than 20% a super-aged society.South Korea is the second country in Asia to reach that milestone after Japan.South Korea, Asia’s fourth-largest economy, entered the aging society classification in 2000 and became an aged society in 2017.한국인 5명 중 1명은 65세 이상으로 대한민국은 급속한 고령화와 세계 최저 출산율이라는 인구학적 문제에 직면해 있다.행정안전부는 한국이 공식적으로 초고령사회에 진입했으며, 65세 이상 인구가 전체 인구의 20%를 넘어섰다고 발표했다.65세 이상 주민등록 인구가 1024만4550명으로, 전체 주민등록 인구 5122만1286명의 20%를 차지했다.유엔에서는 전체 인구 중 65세 이상이 7%를 넘으면 고령화사회, 14%를 넘으면 고령사회, 20% 이상이 되면 초고령사회로 분류한다.한국은 아시아에서 일본에 이어 초고령사회에 진입한 두 번째 국가가 됐다.아시아에서 네 번째로 경제 규모가 큰 한국은 2000년에 고령화사회로 진입했으며, 2017년에는 고령사회가 되었다.해설우리나라는 초고령사회에 접어든 일본, 이탈리아, 독일, 프랑스 등 20여 개국 중 고령화 속도가 가장 빠르다고 합니다. 세계에서 가장 낮은 출산율과 늘어나는 기대수명 때문이