[재미있는 수학] 자동차 상향등의 비밀은 포물선에 있죠

이차곡선과 빛의 관계 ②

포물선과 빛의 성질을 이용하면 빛을 한 방향으로 집중되어 멀리까지 고르게 비춰줄 수도 있고, 멀리에서 오는 전파를 강하게 수신할 수도 있습니다. 포물선과 빛의 성질에 관한 수학적 원리가 적용된 사례를 살펴보면서 수학의 유용성에 대해 느껴보시기 바랍니다.

한경DB

계수가 실수인 두 일차식의 곱으로 인수분해되지 않는 x, y에 대한 이차방정식 Ax2 + By2 + Cxy + Dx + Ey + F=0 (A, B, C, D, E, F는 실수)이 나타내는 곡선을 이차곡선이라 하고, 이차곡선에는 원, 포물선, 타원, 쌍곡선 등이 있습니다. 지난 생글생글 895호의 ‘재미있는 수학’에서는 이차곡선 중 타원과 빛의 성질에 대해서 살펴보았습니다. 이번에는 이차곡선 중 포물선과 빛의 성질에 대해 알아보겠습니다.

어두운 밤에 운전할 때, 자동차의 상향등을 켜면 도로를 넓고 멀리 밝혀주어 운전하기가 편합니다. 이는 자동차의 상향등이 빛을 한 방향으로 집중되어 멀리까지 고르게 비춰주기 때문인데, 여기에 포물선과 빛의 성질에 관한 수학적 원리가 담겨 있습니다.

포물선은 평면 위의 한 점 F와 이 점을 지나지 않는 한 직선 ℓ이 주어질 때, 점 F와 직선 ℓ에 이르는 거리가 각각 같은 점들의 집합이고, 점 F를 포물선의 초점, 직선 ℓ을 포물선의 준선이라고 합니다. 이때 포물선의 초점 F를 지나고 준선 ℓ에 수직인 직선을 포물선의 축, 포물선과 축의 교점을 포물선의 꼭짓점이라고 합니다.

그림1

포물선을 축 둘레로 회전시켜서 얻어지는 곡면을 포물면이라 하고, 포물면의 안쪽을 반사면으로 하는 오목거울을 포물경이라고 하는데, 포물선의 초점에서 나간 빛은 포물면에 반사되어 포물경의 축과 평행하게 나갑니다. 이를 이용해 한 방향만 밝게 비추도록 고안한 것이 자동차의 상향등입니다.

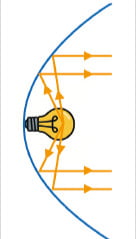
포물선과 빛의 성질은 빛이 최단 경로로 진행한다는 페르마의 법칙과 입사각과 반사각이 같도록 반사된다는 반사의 법칙에서 나옵니다. [그림1]과 같이 포물선의 초점에서 출발한 빛이 포물선에 반사되어 축과 평행하게 지나는 빛의 경로에 관한 수학적 원리를 알아봅시다.

그림2

[그림2]와 같이 초점이 점 F(p, 0)인 포물선 y2=4px(p＞0) 위의 한 점 P(x1, y1)에서의 접선이 x축과 만나는 점을 T라고 할 때, 접선 위의 점 Q와 점 P를 지나고 x축에 평행한 직선 위의 점 X에 대하여 ∠TPF=∠QPX임을 증명하면 됩니다.

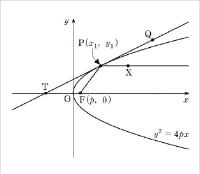
포물선 y2=4px(p＞0 ) 위의 한 점 P(x1, y1)을 지나고 축과 평행한 직선을

라 합시다.

점 P에서의 접선의 방정식은 y1y=2p(x+x1)이고, 이 접선과 x축의 교점인 T는 T(-x1, 0)입니다. 또 y12=4px1이고 P＞0, x1＞0이므로 다음을 얻습니다.

한경DB

입니다. 따라서 삼각형 FPT는 이등변삼각형이므로 ∠TPF=∠PTF입니다.

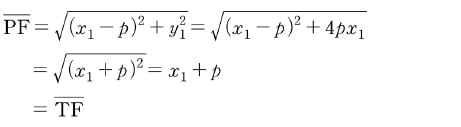
한편,

이므로 ∠PTF=∠QPX입니다.

그러므로 ∠TPF=∠QPX입니다.

이러한 원리가 적용된 사례는 손전등이나 무대의 조명등 등도 있습니다. 이런 성질을 거꾸로 적용하면 포물선의 축과 평행하게 들어온 빛은 포물선에 반사되어 초점에서 모이는 것을 생각할 수 있습니다. 파라볼라 안테나의 단면 모양은 포물선이며, 포물선의 축과 평행하게 들어온 전파는 안테나의 반사기에 반사되어 초점의 위치에 설치된 수신기에 모입니다. 파라볼라 안테나는 멀리에서 오는 전파를 수신할 때 적합해 주로 위성 방송 수신이나 마이크로파 중계에 사용합니다.

Getty Images Bank

이러한 포물선과 빛의 성질을 처음 이용한 사람은 아르키메데스(Archimedes, B.C. 287? ~B.C. 212)라고 합니다. 아르키메데스는 수학과 물리학을 이용해 많은 발명품을 만들었습니다. 당시 아르키메데스의 고국인 시라쿠사는 로마에 끝까지 대항했습니다. 이때 아르키메데스는 새로운 무기를 발명해 수적 열세를 극복하고 전투를 승리로 이끌기도 했습니다. 아르키메데스가 개발한 무기 가운데 하나가 대형 거울이었는데, 포물면 모양으로 만든 이 대형 거울로 태양 빛을 모아 바다에 떠 있는 로마군의 배를 불태웠다는 이야기가 전해 내려옵니다.

홍창섭 경희여고 교사

지금까지 포물선과 빛의 성질에 관한 수학적 원리를 알아보았는데, 이것도 참 신기하고 유용한 것 같습니다. 다음번에는 이차곡선 중 쌍곡선에 관한 수학적 원리에 대해 알아보겠습니다.