생글생글

학습 길잡이 기타

자동차 상향등의 비밀은 포물선에 있죠

계수가 실수인 두 일차식의 곱으로 인수분해되지 않는 x, y에 대한 이차방정식 Ax2 + By2 + Cxy + Dx + Ey + F=0 (A, B, C, D, E, F는 실수)이 나타내는 곡선을 이차곡선이라 하고, 이차곡선에는 원, 포물선, 타원, 쌍곡선 등이 있습니다. 지난 생글생글 895호의 ‘재미있는 수학’에서는 이차곡선 중 타원과 빛의 성질에 대해서 살펴보았습니다. 이번에는 이차곡선 중 포물선과 빛의 성질에 대해 알아보겠습니다.어두운 밤에 운전할 때, 자동차의 상향등을 켜면 도로를 넓고 멀리 밝혀주어 운전하기가 편합니다. 이는 자동차의 상향등이 빛을 한 방향으로 집중되어 멀리까지 고르게 비춰주기 때문인데, 여기에 포물선과 빛의 성질에 관한 수학적 원리가 담겨 있습니다.포물선은 평면 위의 한 점 F와 이 점을 지나지 않는 한 직선 ℓ이 주어질 때, 점 F와 직선 ℓ에 이르는 거리가 각각 같은 점들의 집합이고, 점 F를 포물선의 초점, 직선 ℓ을 포물선의 준선이라고 합니다. 이때 포물선의 초점 F를 지나고 준선 ℓ에 수직인 직선을 포물선의 축, 포물선과 축의 교점을 포물선의 꼭짓점이라고 합니다.포물선을 축 둘레로 회전시켜서 얻어지는 곡면을 포물면이라 하고, 포물면의 안쪽을 반사면으로 하는 오목거울을 포물경이라고 하는데, 포물선의 초점에서 나간 빛은 포물면에 반사되어 포물경의 축과 평행하게 나갑니다. 이를 이용해 한 방향만 밝게 비추도록 고안한 것이 자동차의 상향등입니다.포물선과 빛의 성질은 빛이 최단 경로로 진행한다는 페르마의 법칙과 입사각과 반사각이 같도록 반사된다는 반사의 법칙에서 나옵니다. [그림1]과 같이 포물선의 초점에서 출발한 빛이 포물선에 반사되어 축과 평행하게 지나는

학습 길잡이 기타

수술 없이 몸 속 결석 분쇄, 타원의 성질 이용했죠

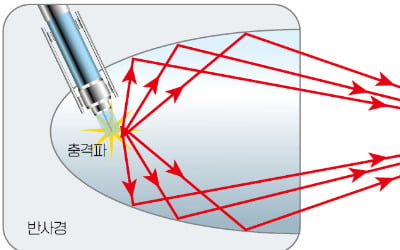
얼마 전 지인이 신장결석으로 고생한다는 이야기를 들었습니다. 신장의 결석을 빼내기 위해 수술을 해야 하느냐고 물었더니, 체외충격파 쇄석술이라는 치료를 하면 수술을 하지 않아도 된다고 했습니다. 그 방법이 신기해 알아보니 이 치료법에 이차곡선 중 타원과 빛의 성질에 관한 수학적 원리가 담겨 있었습니다.이 치료법에는 체외충격파 쇄석기라는 장치가 사용됩니다. 이 장치는 몸속에 생긴 결석을 수술하지 않고 제거할 수 있게 해주는데, 이 장치에서 반사경의 단면 모양은 타원의 일부분입니다.타원은 평면 위의 서로 다른 두 점 F와 F에서의 거리 합이 일정한 점들의 집합이고, 두 점 F와 F′을 타원의 초점이라고 합니다. 결석이 타원의 한 초점에 오도록 맞추고 다른 초점에서 충격파를 발생시키면 반사경에 반사된 충격파가 결석에 모여 신체 조직에 손상을 주지 않으면서 결석을 분쇄합니다. 이에 관한 수학적 원리를 알아봅시다.오른쪽 그림과 같이 두 초점이 F, F인 타원 위의 한 점 P에서 접선 ℓ을 그을 때 접선 ℓ이 두 선분 FP, FP와 각각 이루는 각 θ1과 θ2가 같아짐을 보이면, 초점 F를 출발하여 점 P에서 반사되는 빛은 입사각과 반사각이 같아지므로 초점 F을 지나는 것을 알 수 있습니다.이를 설명하기 위해 초점 F를 접선 ℓ에 대하여 대칭이동한 점을 F이라 하고, 접선 위의 또 다른 점 Q를 잡읍시다. 이때 이고, 두 초점에서 타원 위의 점까지 거리의 합은 항상 일정하므로 입니다. 따라서 … ①이 성립합니다.한편 점 F은 점 F을 접선 ℓ에 대해 대칭이동한 점이므로 이고, 이를 식 ①에 대입하면 입니다. 즉 두 정점 F과 F에서 접선 위의 임의의 점까지 거리의

최준원의 수리 논술 강의노트

출제율 높은 '이차곡선'부터 개념 정리 잘해야

2024학년도에 기하를 출제한 대학은 연세대, 한양대, 중앙대 등 9개 대학으로 이 중 ‘이차곡선’을 출제한 대학은 한양대, 중앙대, 경희대, 홍익대, 동국대, 고대 세종(약학)이다. ‘벡터’를 출제한 대학은 연세대, 한양대, 경희대,시립대고, ‘공간도형’을 출제한 대학은 한양대, 중앙대, 경희대, 고대 세종(약학), 부산대다(표 참조). 전반적인 기하 출제 경향을 보면 기하 교과서 전 단원에 걸쳐 고르게 출제되고 있음을 알 수 있다. 이차곡선은 그중에서도 기하의 가장 기본이 되는 단원으로 출제율 또한 높다. 기하 수리논술을 대비하려는 학생들은 제일 먼저 이차곡선부터 꼼꼼하게 정리하는 것이 필요하다. ▶ 기하 수리논술 대비 포인트 ◀1. 출제율이 가장 높은 이차곡선-포물선,타원,쌍곡선의 정의와 초점 공식을 암기할 것.2. 기하 교과서 또는 EBS 교재 (기하 특강 - Level 1,2 위주) 등을 활용하여 개념 학습3. 위의 24’ 기하 출제문항 분석표의 기하 기출문항을 예시답안을 참조하여 반복 풀이할 것.