[재미있는 수학] 수술 없이 몸 속 결석 분쇄, 타원의 성질 이용했죠

이차곡선과 빛의 관계 ①

신장결석에 걸린 사람의 몸속에 생긴 결석을 수술하지 않고 제거할 수 있습니다. 타원과 빛의 성질에 관한 수학적 원리가 적용된 사례를 살펴보면서 수학의 유용성에 대해 느껴보시기 바랍니다.

얼마 전 지인이 신장결석으로 고생한다는 이야기를 들었습니다. 신장의 결석을 빼내기 위해 수술을 해야 하느냐고 물었더니, 체외충격파 쇄석술이라는 치료를 하면 수술을 하지 않아도 된다고 했습니다. 그 방법이 신기해 알아보니 이 치료법에 이차곡선 중 타원과 빛의 성질에 관한 수학적 원리가 담겨 있었습니다.

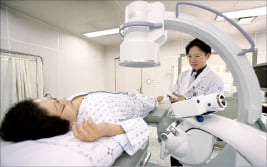
이 치료법에는 체외충격파 쇄석기라는 장치가 사용됩니다. 이 장치는 몸속에 생긴 결석을 수술하지 않고 제거할 수 있게 해주는데, 이 장치에서 반사경의 단면 모양은 타원의 일부분입니다.

타원은 평면 위의 서로 다른 두 점 F와 F에서의 거리 합이 일정한 점들의 집합이고, 두 점 F와 F′을 타원의 초점이라고 합니다. 결석이 타원의 한 초점에 오도록 맞추고 다른 초점에서 충격파를 발생시키면 반사경에 반사된 충격파가 결석에 모여 신체 조직에 손상을 주지 않으면서 결석을 분쇄합니다. 이에 관한 수학적 원리를 알아봅시다.

오른쪽 그림과 같이 두 초점이 F, F인 타원 위의 한 점 P에서 접선 ℓ을 그을 때 접선 ℓ이 두 선분 FP, FP와 각각 이루는 각 θ1과 θ2가 같아짐을 보이면, 초점 F를 출발하여 점 P에서 반사되는 빛은 입사각과 반사각이 같아지므로 초점 F을 지나는 것을 알 수 있습니다.

이를 설명하기 위해 초점 F를 접선 ℓ에 대하여 대칭이동한 점을 F이라 하고, 접선 위의 또 다른 점 Q를 잡읍시다. 이때

이고, 두 초점에서 타원 위의 점까지 거리의 합은 항상 일정하므로

입니다. 따라서

… ①이 성립합니다.

한편 점 F은 점 F을 접선 ℓ에 대해 대칭이동한 점이므로

이고, 이를 식 ①에 대입하면

입니다. 즉 두 정점 F과 F에서 접선 위의 임의의 점까지 거리의 합이 최소가 되는 점은 접점 P입니다.

따라서 세 점 F, P, F은 같은 직선 위에 있게 되고, 직선 PF과 접선이 이루는 각은 θ2와 맞꼭지각이므로 θ2와 같아집니다. 따라서 θ1과 θ2는 같게 되고 점 P를 지나는 접선 ℓ에 대하여 입사각과 반사각이 같아집니다.

타원의 두 초점 F와 F을 지나는 직선을 축으로 하여 타원을 회전시키면 럭비공과 비슷하게 생긴 타원면을 얻습니다. 이때 축을 포함하는 어떤 평면으로 잘라도 그 단면은 타원이며, 이렇게 얻어진 타원의 두 초점은 항상 F와 F이 됩니다.

중앙대병원 체외 충격파 쇄석기. 한경DB

이 외에도 이러한 수학적 원리가 적용된 사례는 많습니다. 치과에서 사용하는 조명을 사용하면 입안을 자세히 살펴볼 수 있습니다. 여기에는 타원을 회전시켜 만든 반사경을 통해 타원의 한 초점에서 출발한 빛이 타원면에 반사되어 다른 한 초점에 빛이 모이는 성질이 이용됩니다. 또한 영국 런던의 성바오로대성당에 있는 ‘속삭이는 회랑(Whispering Gallery)’(회랑이란 원형 모양의 복도를 의미함)에서는 이 성당 돔 아래의 회랑 한쪽에서 속삭이는 소리가 회랑의 건너편 한 지점에서 더 잘 들립니다. 이것도 돔을 이루는 천장이 타원면으로 이루어져 있기 때문입니다. 타원의 한 초점에 해당하는 곳에서 소리를 내면 이 소리는 사방으로 퍼지지만 타원형 천장에 도달해 반사된 소리가 모두 건너편 초점에 해당하는 위치에 다시 모이게 되므로 그 소리가 또렷하게 들리는 것입니다. 이러한 신비한 현상이 일어나는 곳은 미국 국회의사당의 조각홀(Statuary Hall), 튀르키예 블루모스크, 중국 천단공원 등이 있습니다.

홍창섭 경희여고 교사

지금까지 타원과 빛의 성질에 관한 수학적 원리를 알아보았는데, 참 신기하고 유용한 것 같습니다. 다음번에는 이차곡선 중 포물선에 관한 수학적 원리에 대해 알아보겠습니다.