전체뉴스
-
테샛 공부합시다
고교 대상 원주금융회계高 신동혁···주니어테샛 1등은 방산中 두예인
테샛관리위원회는 최근 70회 테샛 성적 평가회의를 열고 부문별 성적 우수자를 확정해 테샛 홈페이지에 발표했다. 응시자들은 개인별 자격 등급과 성적표를 테샛 홈페이지에서 출력할 수 있다. 원주금융회계고 약진 두드러져 테샛 70회 시험 고교 개인 대상은 원주금융회계고 2학년에 재학 중인 신동혁 학생이 수상했다. 최근 고교 부문에서는 S등급 대상 수상자가 잇따라 나와 경제 교육에 관한 관심을 반영하고 있다. 2등인 최우수상은 서울여자상업고 2학년...
-
과학과 놀자
얼굴로 스마트폰 잠금해제…어떻게 감지·구별하나
최근 휴대폰엔 암호나 지문 대신 얼굴을 인식해 잠금을 해제하는 페이스 아이디(Face ID) 기능이 있다. 또 많은 사람이 본인의 모습을 특색 있게 남기기 위해 눈, 코, 입의 위치를 인식하는 앱을 사용하기도 한다. 이러한 작업을 위해서는 컴퓨터, 즉 기계가 이미지 정보를 인식해 얼굴 영역을 파악하고 또 그에 더해 눈, 코, 입의 위치를 파악해야 한다. 컴퓨터는 어떻게 우리 얼굴을 감지하는 것일까? 확실하게 말할 수 있는 것은 사람이 물체를 ...
-
신철수 쌤의 국어 지문 읽기
알고 있어야 할 전의적 의미와 알아내야 할 개념
헤겔에게서 변증법은 논증의 방식임을 넘어, 논증 대상 자체의 존재 방식이기도 하다. 즉 세계의 근원적 질서인 ‘이념’의 내적 구조도, 이념이 시·공간적 현실로서 드러나는 방식도 변증법적이기에, 이념과 현실은 하나의 체계를 이루며, 이 두 차원의 원리를 밝히는 철학적 논증도 변증법적 체계성을 지녀야 한다. - 2022학년도 대학수학능력 시험 - 변증법은 논증의 방식임을 넘어, 논증 대상 자체의 존재 방식이기도...
-
대입 전략
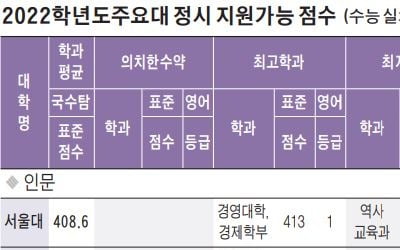
서울대 경영·경제 413점···의예과는 430점, 연세대·고려대 인문 최저 389점·자연 401점
올해 수능은 국어, 수학, 영어가 모두 어렵게 출제되면서 역대급 불수능으로 꼽힌다. 여기에 국어, 수학 선택과목에 따른 유불리가 현실화되면서 정시 최종지원전략 셈법은 더 복잡해졌다. 이과생 중 상당수가 인문계 학과로 교차지원에 나설 것으로 예상되는 가운데 눈치작전도 심할 것으로 보인다. 자신의 객관적 위치를 정확히 알고 최종 지원전략을 꼼꼼하게 점검할 때다. 2022학년도 수능 실채점 기준 정시 지원가능 점수를 분석해본다. 표준점수 기준 서울...
-
대학 생글이 통신
그동안의 공부 태도 점검···부족한 부분 보강을
2학기 기말고사가 끝나면 다음 학년으로 진학하기 전까지 2~3개월 정도의 시간적 여유가 생깁니다. 이번 글에서는 제 경험을 살려 겨울방학 때 할 수 있는 것들에 대해 이야기해보고자 합니다. #1.배운 내용 복습하기 이번 학년 때 배운 내용은 다음 학년 때 배울 내용을 이해하기 위한 기반이 됩니다. 배운 내용만큼은 충분히 숙지하고 넘어가야 합니다. 배운 내용을 얼마나 이해하고 있는지 확인하기 위해선 수업 시간에 활용한 교과서와 학습지를 복습해...
-
사진으로 보는 세상
2024 파리올림픽 개회식은 센강에서
파리올림픽 조직위원회는 2024년 7월 26일 파리올림픽 개회식을 스타디움이 아니라 센강에서 열 것이라고 밝혔다. 파리에서 토니 에스탕게 2024 파리올림픽·패럴림픽 조직위원장이 지난 13일 올림픽 개회식과 관련해 기자회견을 하고 있다. 연합뉴스
-
생글기자
겨울 운동팁 3가지 지키고 집콕 확찐자 탈출하자
요즘 같은 겨울철엔 실외 활동이 줄어들고 몸이 움츠러들기 쉽다. 날씨가 추울수록 운동을 꾸준히 해야 체력을 유지하고 독감 기관지염 등 겨울철 질병에 대한 면역력을 키울 수 있다. 단, 날씨가 추운 만큼 몇 가지 주의할 사항이 있다. 첫째, 겨울철에는 운동을 할 때도 옷을 따뜻하게 입어야 한다. 이때 두꺼운 패딩 하나를 걸치는 것보다는 얇은 옷을 여러 벌 겹쳐 입는 것이 좋다. 옷과 옷 사이의 공기층이 체온 유지를 돕는다. 통풍이 되지 않는 땀...
-
최준원의 수리 논술 강의노트
출제 빈도 높은 수학적 귀납법 증명 문제
수학적 귀납법 증명 문제는 구조와 채점포인트가 비교적 명확하기 때문에 출제 빈도가 높고 변별력도 갖춘 수리논술의 주요 출제 유형이다. n=k일 때 가정한 식으로부터 n=k+1일 때의 식을 보이려고 하는 과정이 핵심 채점포인트이며 이때 가정한 식과 보이려는 식을 확실하게 구분해서 문장으로 표현하는 것이 중요하다. 포인트 수리논술을 시작하는 수험생들은 수학, 수학Ⅰ, 수학Ⅱ의 기본 논증추론 과정을 직접 자신의 손으로 써보고 익히는 과정부터 시작...