#생글생글
-
대학 생글이 통신
'리버럴 아츠 칼리지'를 아시나요
리버럴 아츠 칼리지를 들어본 적이 있나요. 저는 다소 생소한 리버럴 아츠 칼리지를 소개하려고 합니다. 리버럴 아츠 칼리지란 인문학 및 순수 자연과학 분야의 학부 과정, 즉 리버럴 아츠를 중점적으로 다루는 대학입니다. 기술 습득과 달리 폭넓은 일반 지식을 배우며 일반적인 지적 능력을 개발하는 것을 목표로 합니다. 리버럴 아츠 칼리지는 우리가 흔히 아는 대학교처럼 학과가 정해져 있지 않고 하버드, 스탠퍼드, UCLA 같은 종합대학(universi...
-
대학 생글이 통신
수시원서 접수를 완료한 후 알아야 할 것들
수시모집 원서 접수에 이어 전형이 시작됐습니다. 저도 수시로 대학 입시를 치른 사람으로서 이 시점에 꼭 알아두면 좋을 것들에 대해 말해보려 합니다. 먼저, 원서 접수 자체를 빨리 잊는 것입니다. 공부를 하다 보면 문득 ‘나 여기 원서 넣었지’ ‘내가 할 수 있을까’ ‘잘못 쓴 건 아닐까’ 등의 생각이 꼬리를 물며 집중력을 흐트러뜨릴 거예요. 저도 비슷한 경험을 했습니다. 원서를 ...
-
진학 길잡이 기타
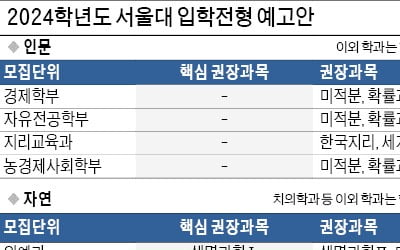
서울대, 2024학년도부터 모집단위별 고교 권장과목 지정
문·이과 통합, 선택수업 확대를 위시한 ‘2015개정교육과정’과 고교학점제 등 고등학교 현장이 큰 변화를 맞고 있다. 이에 맞춰 서울대는 2023학년도 정시에 교과평가 도입, 2024학년도 전공 연계 교과이수 과목 지정 등 입학전형에 변화를 예고하고 있다. 전공 연계 교과이수 과목은 해당 모집단위에서 고교 재학 중 학교 수업을 통해 이수하기를 권하는 과목이다. 서울대 입시에서 진로, 적성에 맞춰 수업을 선택해 ...
-
홍성호 기자의 열려라 우리말
'단기필마'와 '애매모호'…같으면서 다른 점
삼국지에서 조자룡이 조조 군에 갇힌 유비의 아들을 구출해오는 대목은 손에 땀을 쥐게 하는 명장면이다. 말 한 필에 의지해 홀로 적진을 돌파하는 조자룡의 위용은 ‘단기필마’를 얘기할 때 자주 인용된다. 하지만 이 말은 사전에 나오지 않는다(이하 표준국어대사전 기준). ‘단기+필마’의 결합인데, 합성어로 처리되지 않았다. 둘 다 겹말이지만 사전 처리는 서로 달라 대신에 ‘단기’와 ...
-
신철수 쌤의 국어 지문 읽기
3인칭 시점 소설의 내적 독백…인물의 심리 표현 방법
[앞부분 줄거리] 차나 한잔 하자는 신문사 문화부장으로부터 해고 통보를 받은 그는 다른 신문사의 문화부장을 찾아가 차나 한잔 하면서 일자리를 부탁한다. 그러나 문화부장은 돈을 쓰지 않는 사장을 핑계로 부탁을 거절한다. 그는 만화가인 김 선생을 만나 술을 마신다. “다방에 가서 그 양반이 그러더군요. 사람 웃기는 방법의 몇 가지 패턴을 안다고 곧 만화가가 되는 것이 아니다. 바로 그 양반이 그랬어요. 두꺼비 같은 눈알을 부라리면서 말...
-
생글기자
쓰레기로 몸살 앓는 지구 살리기운동 '제로 웨이스트'
코로나19로 인해 배달 및 포장 서비스가 급증하고, 바이러스를 차단하기 위한 마스크와 위생장갑 폐기물 등 쓰레기가 늘면서 각종 쓰레기 문제를 해결해야 한다는 목소리가 커지고 있다. 이를 위한 캠페인이 ‘제로 웨이스트(zero waste)’ 챌린지다. 제로 웨이스트란 모든 제품이 재사용될 수 있도록 장려하며, 폐기물을 방지하는 데 초점을 맞춘 원칙을 말한다. 즉, 쓰레기 배출량을 줄여 낭비가 ‘0’이 ...
-
생글기자
중국 헝다그룹발 위기에 대응방안 마련해야
중국의 제2 부동산 개발업체이자 글로벌 500대 기업 중 하나인 헝다그룹이 위기에 몰려 있다. 파산설에 휩싸인 헝다그룹은 지난 4일 홍콩증시에서 거래가 정지됐다. 블룸버그통신 등에 따르면 헝다그룹과 헝다의 부동산 관리사업 부문인 헝다물업 주식의 홍콩증시 거래가 잠정 중단됐다. 급성장하던 헝다그룹이 위기를 맞이하게 된 원인은 최근 중국 아파트가 포화상태에 이르면서부터다. 부채를 빌려 다양한 사업을 무리하게 펼치던 헝다그룹은 최근 자금경색이 오면...
-
스도쿠 여행
스도쿠 여행 (605)