#홍성호 기자의 열려라\! 우리말
-
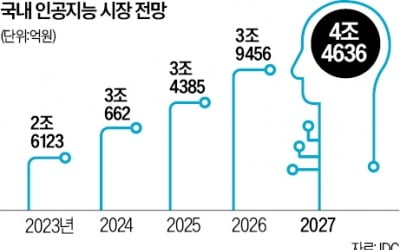
숫자로 읽는 세상
한국 오는 나델라 MS 최고경영자, 현대차·포스코·KT와 'AI 동맹' 맺나
2년 만에 한국을 찾는 사티아 나델라 마이크로소프트(MS) 최고경영자(CEO)가 현대자동차, 포스코, 신한금융, KT 등 국내 간판 기업 경영진과 회동을 추진한다. 전 세계 인공지능(AI) 시장이 가파르게 성장하는 상황에서 한국 기업과의 협업 기회를 확대하기 위해서다. 나델라 CEO가 딥시크 출현으로 주목받는 저비용 고성능 AI 모델에 맞선 MS의 AI 기술 청사진을 제시할 가능성이 크다는 관측이 나온다.11일 업계에 따르면 나델라 CEO는 다음 달 26일로 예정된 ‘마이크로소프트 AI 투어 인 서울’ 행사에 참석한다. 그가 한국을 찾는 것은 2022년 11월 이후 2년여 만이다.세계 각국을 돌며 여는 마이크로소프트 AI 투어는 자사 신기술과 AI 시장 전망 등을 공유하는 자리다. 나델라 CEO가 전 세계에서 진행하는 AI 투어 가운데 특별히 서울 행사를 택한 것은 급성장하는 한국 시장에 공을 들이기 위해서다. 이 행사는 작년 4월에도 한 차례 열렸다. 당시에는 AI 업계 관계자 및 개발자들이 참석해 신기술 소개, 체험형 워크숍 등의 행사만 진행했다. 업계 관계자는 “이번 서울 행사를 통해 MS의 AI 기술을 활용한 국내 기업의 성공 사례를 공유할 것으로 보인다”며 “특히 나델라 CEO가 직접 기조 연설자로 나서 AI 기술이 전 세계 산업에서 일으킨 변화를 중심으로 메시지를 발표할 가능성이 높다”고 말했다.MS는 나델라 CEO의 전격 방한을 계기로 국내 기업인들과 타운홀 미팅을 할 계획이다. 이를 위해 정의선 현대차그룹 회장, 장인화 포스코그룹 회장, 진옥동 신한금융그룹 회장, 김영섭 KT 대표 등에게 만남을 제안한 것으로 알려졌다. 한국 대표 제조·금융·통신사와 MS 간 협력 방안 및 AI 기술 전망
-
사진으로 보는 세상
성년례와 함께 열린 한복 졸업식
지난 11일 서울 대조동 동명여고에서 열린 102회 졸업식 및 성년례에서 형형색색의 한복을 차려입은 졸업생들이 환하게 웃고 있다. AP연합뉴스
-
영어 이야기
내기 싫은 돈을 억지로 낼 때 'cough up'
해설자판기에 돈을 넣었는데, 음료나 과자가 나오지 않거나 거스름돈이 나오지 않아 당황한 경험이 있나요? 그럴 때 우리는 흔히 “자판기가 내 돈을 먹었다” 또는 “돈을 꿀꺽했다”라고 말하곤 합니다. 영어에도 비슷한 표현이 있습니다. The vending machine ate my money(자판기가 내 돈을 먹어버렸어)라는 말이죠. 이처럼 eat money는 주로 부정한 방법으로 돈을 취득할 때 사용하는 표현입니다.반대로 받은 돈을 강요에 의해 돌려주거나 내기 싫은 돈을 억지로 지불할 때는 어떤 표현을 사용할까요? 우리는 흔히 ‘돈을 토해내다’라는 표현을 쓰기도 합니다. 영어에서도 ‘토해내다’라고 표현해요. ‘기침’을 의미하는 cough를 활용한 cough up money죠. 기침해서 무언가를 밖으로 내보낸다는 의미에서 ‘토하다’는 의미가 되었습니다. 기침을 심하게 하면 배가 아프거나 심지어 피가 나오는 경우도 있어 그리 유쾌한 경험은 아니지요. 이런 이유로 cough up은 ‘내기 싫은 돈을 억지로 내다’라는 의미로 사용하고 있습니다.물론 cough up money 대신 pay money나 give money라고도 쓸 수 있지만, 뉘앙스에 차이가 있습니다. He reluctantly coughed up money he owed his friend(그는 마지못해 친구에게 빌린 돈을 갚았다). 친구가 독촉해서 결국 돈을 돌려줬다는 의미지요.The ruling party has proposed a bill to require banks to cough up a maximum 40% of a bank’s net interest income exceeding 120% of the past five years’ average(여당은 지난 5년 평균의 120%를 초과하는 순이자 소득의 최대 40%를 내도록 요구하는 법안을 제안했습니다).예문에 나온 short selling(공매도)은 가지고 있지 않은 주식을 주어진 기간 내에 증권사에서 빌려
-
국가공인 경제이해력 검증시험 맛보기
비교우위
[문제] A국과 B국이 비교우위에 따라 무역을 하면 해당 국가에 미칠 영향과 관련한 아래의 설명 중 옳은 것을 고르면?ㄱ. 외국 상품이 국내 시장을 왜곡한다.ㄴ. 다양한 상품을 저렴한 가격에 구매할 수 있다.ㄷ. 모든 산업의 근로자는 고용, 실업에 영향을 받지 않는다.ㄹ. 국내 독점 산업의 진입 장벽이 제거되면서 국내 소비자 잉여가 증가한다.① ㄱ, ㄴ② ㄱ, ㄷ③ ㄴ, ㄷ④ ㄴ, ㄹ⑤ ㄷ, ㄹ[해설] 한 생산자가 다른 생산자보다 낮은 기회비용으로 어떤 재화를 생산할 수 있을 때 그 재화 생산에 비교우위가 있다고 말한다. 비교우위에 따라 자유무역을 하면 해외의 저렴하고 품질 좋은 물건이 들어오고 독점인 국내 산업 분야의 진입장벽이 제거되면서 국내 소비자잉여가 증가한다. 하지만 교역 과정에서 비교열위에 있는 국내 산업의 실업자가 늘어나면서 일부 산업과 근로자들이 영향을 받는다. 정답 ④[문제] 금융 산업에서 도덕적 해이의 사례가 아닌 것은?① 거래 당사자 사이에 정보 비대칭이 없는 경우에는 발생하지 않는다.② 금융거래가 이뤄지기 전에 대부자가 차입자의 위험 수준을 파악할 수 없다.③ 금융거래 계약 후 차입자가 자금을 원래의 목적대로 이용하지 않을 때 발생한다.④ 금융기관의 경영에 대해 주주와 경영자가 서로 다른 목적을 가지고 있을 때 발생한다.⑤ 금융거래 계약 후 대부자가 차입자의 행동을 더 효과적으로 감시할 수 있다면 도덕적 해이가 줄어들 수 있다.[해설] 도덕적 해이란 감춰진 행동의 상황에서 어떤 거래가 이뤄진 이후 정보를 가진 측이 바람직하지 못한 행동을 하는 현상이다. 도덕적 해이는 주인-대리인 문제로 연결된다. 주주와 경영자의 관계처럼 주인은 대리
-
경제·금융 상식 퀴즈
2월 17일 (880)
1. 네이버 창업자인 ‘이 사람’이 8년 만에 이사회 의장을 맡아 경영에 복귀하기로 했다. ‘은둔의 경영자’라는 별명이 붙은 이 사람은?① 이해진 ② 김범수③ 김택진 ④ 방시혁2. 우물 안 개구리처럼 자국 사정에만 맞춰 기술을 발전시키다가 세계 시장에서 고립되는 현상을 가리키는 말은?① 스태그플레이션 ② 디폴트③ 갈라파고스 ④ 모라토리엄3. 다음 중 적대적 인수합병(M&A)으로부터 기존 경영진의 경영권을 보호하기 위한 수단으로 활용되는 것은?① 공모주 ② 황금주③ 동전주 ④ 주도주4. 상장사들이 주가 관리를 위해 ‘이것’을 매입 후 소각하는 사례가 늘고 있다. 회사가 발행한 주식을 회사가 취득해 보유 중인 이것은?① 우선주 ② 자사주③ 황제주 ④ 실권주5. 세율이 적정 수준 이상으로 올라가면 경제주체들의 의욕이 감소해 세수가 오히려 줄어든다는 점을 보여주는 것은?① 수요공급곡선 ② 필립스곡선③ 로렌츠곡선 ④ 래퍼곡선6. 대만에 본사를 둔 파운드리 기업으로, 대만 내에서 일명 ‘실리콘 실드’ 역할을 하는 기업의 이름은?① 폭스콘 ② ASML③ TSMC ④ 엔비디아7. 국내 주요 은행이 정기 예·적금, 금융채, 양도성예금증서 등으로 시장에서 자금을 조달하는 평균비용을 보여주는 지표는?① COFIX ② NIM③ ATS ④ ROA8. 다음 중 ‘죄수의 딜레마’ 원리를 이론적 토대로 삼아 운영되고 있는 제도는?① 네거티브 규제 ② 기업결합심사③ 국부펀드 ④ 리니언시▶정답 : 1 ① 2 ③ 3 ② 4 ② 5 ④ 6 ③ 7 ① 8 ④
-
시사 이슈 찬반토론
'노인 연령' 기준, 이번엔 높여야 하나
보건복지부가 올해 업무계획에서 현재 65세인 노인 연령 기준을 높이는 논의를 본격 착수하겠다는 방침을 밝혔다. 과거와 달리 신체가 건강하고 경제력을 갖춘 노인이 크게 늘었기 때문이다. 노인 연령은 1981년에 제정된 노인복지법을 기준으로 할 때 40년 넘게 만 65세 그대로 유지돼왔다. 노인 지하철 무임승차 논란이 촉발한 노인 연령 기준과 관련해 대한노인회는 지난해 노인 연령 기준을 75세로 단계적으로 조정하자고 제안했다. 인구 중 65세 이상이 전체의 20%에 육박한다. 늘 제자리를 맴돈 노인 연령 기준 상향 논란이 이번에는 매듭지을 수 있을지 주목된다. [찬성] 이대로면 50년 뒤 1명이 1명 부양…기준 개선해 후세대 부담 줄여야사회적으로 ‘노인’이라고 인식하는 연령이 크게 높아졌다. 현행 기준은 평균수명이 60대에 머물던 시대에 만들어졌다. 노인복지법 제정 당시 66.1세이던 한국인의 평균수명이 83.6세로 늘었다(2023년 기준). 한국 사회는 2017년 고령사회(65세 이상 고령자가 전체 인구의 14% 이상)에 접어들었다. 통계청에 따르면 지난해 65세 이상 고령 인구는 993만8000명으로 전체의 19.2%를 차지했다. 올해 초고령사회(20% 이상) 진입이 확실시된다.수명뿐 아니라 건강도 좋아졌다. 요즘 60대는 자신을 정신적으로나 신체적으로나 늙었다고 인식하지 않는다. 경제력도 과거 노인과 다르다. 복지부가 지난해 10월에 발표한 노인실태조사에 따르면 새로 노인 연령에 진입한 65~69세 가구의 연간 총소득은 4787만원으로 전체 65세 이상 평균 3469만원보다 38%이나 높았다. 부동산(3억3600만원)과 금융 자산(5500만원) 등 보유 자산도 4억원이 넘어 다른 연령대에 비해 상당히 많았다. 요즘 60대는 대
-
학습 길잡이 기타
위상기하학에선 접시와 컵이 다 같은 모양이죠
지난 생글생글 878호에서 비유클리드기하학을 소개하며 더 많은 기하학이 있다고 했는데요, 오늘은 언급한 것처럼 좀 더 다양한 기하학을 이야기하도록 하겠습니다.보통 우리는 정해진 규칙 안에서 사고를 전개하는 데 익숙합니다. 특히 수학 문제를 풀 때 그렇죠. 하지만 일부 선생님은 수학 문제를 직접 만들어보라고 권하기도 합니다. 한편 어떤 수학 문제는 그 문제에서만 사용되는 특정한 조건이나 기호를 포함하기도 하죠. 이런 상황은 여러분에게 새로운 고민거리를 안겨주기도 하지만, 동시에 우리가 어디까지, 무엇을 할 수 있는지 생각해보는 실마리가 되기도 합니다.기하학에서도 마찬가지입니다. 이미 소개했듯이, 유클리드기하학이란 거의 완벽에 가까운 체계가 있고 이 규칙을 지키며 생각과 추론을 이어나갈 수 있습니다. 그러나 우리가 직접, 이 규칙을 수정할 수도 있다는 것이죠. 사실 기하학에서는 이 사실을 깨닫는 것 자체가 아주 오래 걸린 일이었습니다.첫 번째로 사영기하학을 소개할까 합니다. 국내에는 많이 알려져 있지 않지만 수학 관련 교양서적에서 꾸준히 찾아볼 수 있는 기하학인데요, 위에서도 언급했지만 새로운 규칙을 만들어야 한다는 점에서 이 기하학은 ‘무한하게 먼 곳’을 실제로 있는 것처럼 가정하고 논리를 전개합니다. 이 말은 한 쌍의 평행선이 있을 때 그 두 선의 교점이 아주 먼 곳에 ‘있다’라고 가정한다는 의미입니다. 당연한 이야기지만 옆에 보이는 그림과 같이, 2개 직선은 하나의 교점을 가집니다.이때 교점 A는 두 직선이 평행선에 가까워지면서 점점 오른쪽으로 밀려나는데, 결국 평행선이 되는 순간 교점 A는 갈 곳이 없어지죠. 그런데 오
-
신동열의 고사성어 읽기
一葉知秋 (일엽지추)
▶한자풀이一: 한 일 葉: 잎 엽 知: 알 지 秋: 가을 추나뭇잎 하나로 가을이 옴을 알다작은 일을 가지고 올 일을 미리 짐작함 -<회남자(淮南子)><회남자(淮南子)는 전한의 회남왕 유안(劉安)이 빈객들을 모아 편찬한 일종의 백과사전이다. 모두 21권으로 되어 있으며, <여씨춘추(呂氏春秋)>와 함께 제자백가 중 잡가(雜家)의 대표작이다.<회남자> 설산훈 편에는 “작은 것으로 큰 것을 밝히고, 나뭇잎 하나 지는 것을 보고 가을이 옴을 알고(一葉知秋), 병 속의 얼음을 보고서 세상이 추워졌음을 알 수 있노라”하는 구절이 있다. 여기에서 유래한 일엽지추(一葉知秋)는 낙엽 하나로 가을이 오는 것을 안다는 뜻으로, 작은 일로 장차 다가올 일을 미리 짐작한다는 말이다. 당나라 시에도 “산의 중은 여러 갑자년을 풀지 못하지만, 나뭇잎 하나가 지는 것으로 가을이 돌아왔음을 안다(山僧不解數甲子 一葉落知天下秋)”는 구절이 나온다.<논어>에 나오는 일이관지(一以貫之)도 함의가 비슷하다. 공자가 자공에게 물었다. “자공아, 너는 내가 많은 걸 배워서 그걸 안다고 생각하느냐?” 자공이 “당연히 그렇지 않습니까”라고 답하니 공자가 말했다. “아니다. 나는 하나의 이치를 꿰어서 알고 있느니라(一以貫之).” 이는 하나의 이치를 꿰면 나머지는 절로 따라온다는 뜻이다. 흔히 도가 깊은 스님은 방 안에 앉아서도 사계가 바뀌는 것을 안다고 했는데 일엽지추, 일이관지와 뜻이 하나로 이어진다.통찰은 작은 조짐으로 큰 변화를 읽을 줄 아는 힘이다. 지식과 경험, 사유가 어우러져 통찰력을 키운다. “어리석은 사람은 당해봐도 모르고, 보통