[재미있는 수학] 위상기하학에선 접시와 컵이 다 같은 모양이죠

非유클리드기하학의 확장

기하학은 우리의 상상력을 기반으로 하지만 이를 뛰어넘어 우리의 사고를 상상력 너머로 끌어올릴 수도 있습니다. 그리고 무언가를 안다는 것, 이해한다는 것은 아주 기분 좋은 일이 아닐 수 없습니다.

Getty Images Bank

지난 생글생글 878호에서 비유클리드기하학을 소개하며 더 많은 기하학이 있다고 했는데요, 오늘은 언급한 것처럼 좀 더 다양한 기하학을 이야기하도록 하겠습니다.

보통 우리는 정해진 규칙 안에서 사고를 전개하는 데 익숙합니다. 특히 수학 문제를 풀 때 그렇죠. 하지만 일부 선생님은 수학 문제를 직접 만들어보라고 권하기도 합니다. 한편 어떤 수학 문제는 그 문제에서만 사용되는 특정한 조건이나 기호를 포함하기도 하죠. 이런 상황은 여러분에게 새로운 고민거리를 안겨주기도 하지만, 동시에 우리가 어디까지, 무엇을 할 수 있는지 생각해보는 실마리가 되기도 합니다.

기하학에서도 마찬가지입니다. 이미 소개했듯이, 유클리드기하학이란 거의 완벽에 가까운 체계가 있고 이 규칙을 지키며 생각과 추론을 이어나갈 수 있습니다. 그러나 우리가 직접, 이 규칙을 수정할 수도 있다는 것이죠. 사실 기하학에서는 이 사실을 깨닫는 것 자체가 아주 오래 걸린 일이었습니다.

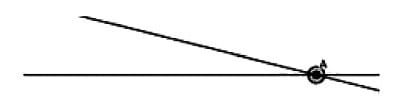
첫 번째로 사영기하학을 소개할까 합니다. 국내에는 많이 알려져 있지 않지만 수학 관련 교양서적에서 꾸준히 찾아볼 수 있는 기하학인데요, 위에서도 언급했지만 새로운 규칙을 만들어야 한다는 점에서 이 기하학은 ‘무한하게 먼 곳’을 실제로 있는 것처럼 가정하고 논리를 전개합니다. 이 말은 한 쌍의 평행선이 있을 때 그 두 선의 교점이 아주 먼 곳에 ‘있다’라고 가정한다는 의미입니다. 당연한 이야기지만 옆에 보이는 그림과 같이, 2개 직선은 하나의 교점을 가집니다.

이때 교점 A는 두 직선이 평행선에 가까워지면서 점점 오른쪽으로 밀려나는데, 결국 평행선이 되는 순간 교점 A는 갈 곳이 없어지죠. 그런데 오른쪽으로 무한하게 밀려나 버린 이 점이 없어지는 것이 아니라 ‘무한대에 있다’고 볼 수도 있지 않을까요? 이러한 규칙을 받아들여 전개하는 기하학을 사영기하학이라고 합니다.

이 가정을 받아들인 사영기하학에서는 정말 말도 안 되는 결과들이 쏟아져 나옵니다. 일단 모든 평행선이 만난다고 볼 수 있겠죠. ③번 그림의 교점 A는 무한대에 있어 볼 수 없을 뿐 존재하기로 한 것이니까요. 또한 무한의 위치를 가정하기에 직선의 양 끝이 이어지게 됩니다. 게다가 무한 위의 점을 삼각형 세 점 중 하나로 둔다면 절대 도형이라고 볼 수 없는 모양도 삼각형이라고 할 수 있게 됩니다.

①

②

③

두 번째로는 위상기하학이 있습니다. 위상기하학은 좀 더 대중적이라고 볼 수 있습니다. 특히 여러 소설이나 웹툰에서 언급하기도 하는 ‘클라인의 병’이라는 특이한 도형이 이 위상기하학과 관련되어 있기도 합니다.

위상기하학에서 새롭게 따르는 규칙은 길이, 넓이, 부피를 전혀 고려하지 않는 것입니다. 어떻게 이어져 있는지만 중점으로 보는 것이죠. 즉 기존의 것을 늘리고 줄이고 비틀어도 같은 것이라고 봅니다. 그 대신 끊거나 이어 붙이거나 자르면 완전히 다른 대상이 되는 것이고요. 이런 측면에서 위상기하학을 ‘고무판 기하학’이라고도 부릅니다.

위상기하학 측면에서는 원판과 축구공은 완전히 같은 것이며, 접시와 손잡이 없는 컵 역시 다 같은 모양으로 취급합니다. 누르고 늘려 같게 만들 수 있기 때문이죠. 그러나 가운데 구멍이 뚫린 도넛은 아무리 줄이고 구부려도 불가능하기에 다른 도형이 되는 것입니다. 극단적으로 보자면 도넛과 손잡이 달린 컵은 위상기하학 입장에서는 같은 도형인 셈이죠.

이정현 푸른숲발도르프학교 교사

이 기하학의 시각으로는 결국 대상에 구멍이 몇 개 있는지, 이 면과 어느 면이 이어져 있는지를 구별하는 것이 가장 중요한 연구 대상이 됩니다. 여러 매체에서 종종 볼 수 있는 유명한 클라인의 병이라는 것은 뫼비우스의 띠와 같은 의미의 도형으로, 안팎의 구분이 없는 병 혹은 대롱 모양의 도형입니다. 위상기하학에서 다루기에 아주 좋은 도형이죠.

그렇다면 우주의 모양은 어떤 모양일까요? 블랙홀은 구멍일까요? 무한하게 펼쳐질까요? 그게 아닌 경우 지구처럼 한쪽으로 가다 보면 출발한 곳으로 올 수 있을까요? 위상기하학은 우리의 상상을 뛰어넘는 이러한 질문들과도 연결되어 있습니다.