[재미있는 수학] 독감 판정받았다고 모두 독감에 걸릴까?

조건부확률

“병원에서 독감에 걸렸다고 판정받은 사람이 실제로 모두 독감에 걸린 것이 맞는 걸까요?”에 대한 답은 조건부확률로 얻을 수 있습니다. 수학을 통해 일상의 질문을 해석하는 과정을 보면서 수학의 유용성을 느껴보길 바랍니다.

뉴스1

지난 겨울에는 유달리 독감 환자가 많았습니다. 그리고 실제로 독감에 걸렸던 이들 중 많은 사람이 이번 독감이 특별히 많이 아팠다고도 말합니다. 그런데 주위에서 보면 병원에서 독감으로 판정받았는데도 전혀 아프지 않고 지나갔다는 사람도 있습니다. 왜 그럴까요? 병원에서 독감에 걸렸다고 판정받은 사람이 실제로 모두 독감에 걸린 것이 맞는 걸까요?

의료 진단 검사에서 양성반응이 나타나면 감염되었음을, 음성반응이 나타나면 감염되지 않았음을 뜻합니다. 그러나 진단 검사용 의료 키트가 항상 정확한 것은 아니어서 감염된 경우에도 음성반응을 나타내기도 합니다. 감염되었을 때 양성반응이 나타날 확률을 그 의료 진단 키트의 민감도라고 하는데, 민감도가 클수록 의료 진단 키트의 정확도는 높다고 할 수 있습니다.

간단한 예를 생각해봅시다. 어떤 바이러스에 감염된 사람에게 양성반응을, 감염되지 않은 사람에게 음성반응을 나타내는 민감도가 0.99인 의료 진단 키트가 있다고 할 때, 이 의료 진단 키트에 의해 양성반응을 나타낸 사람이 실제 감염자일 확률은 얼마나 될까요? 아마도 많은 사람은 그 확률이 0.99라고 성급하게 생각할지도 모르지만 실제 확률은 훨씬 낮습니다.

예를 들어 어느 지역의 인구가 10만 명이고, 그 지역에서 실제 감염된 사람이 100명이라고 가정해봅시다. 의료 진단 키트의 민감도가 0.99라고 하면 다음과 같은 표를 얻을 수 있습니다.

위의 표에서 검사 결과 양성반응을 나타낸 사람은 99+999=1098(명)이고, 이 중 실제 감염자는 99명입니다.

따라서 이 의료 진단 키트에 의해 양성반응을 나타낸 사람이 실제 감염자일 확률은

뉴스1

, 즉 약 0.09에 불과합니다. 이는 이 의료 진단 키트를 통해 양성반응을 나타낸 사람이 실제로 감염자일 확률은 예상보다 낮음을 뜻합니다. 따라서 한 가지 검사로 감염이 의심된다면 다른 검사를 추가로 받을 필요가 있습니다.

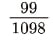
그러면 처음 질문인 “병원에서 독감에 걸렸다고 판정받은 사람이 실제로 모두 독감에 걸린 것이 맞는 걸까요?”에 대한 답이 되었죠?

이와 관련된 수학 개념은 ‘베이즈의 정리’입니다. 이 정리는 이미 주어진 확률을 이용해 새로운 확률을 계산하는 공식입니다. 영국의 목사이자 수학자인 베이즈(Bayes, T., 1702~1761)가 처음 발견했습니다. 그의 이론은 두 사건 A와 B에 대하여 P(A), P(B), P(A|B)를 알 때, 확률 P(B|A)를

와 같이 계산할 수 있다는 것입니다. 베이즈의 정리는 다양한 분야에서 적용되고 있는데, 특히 컴퓨터공학 분야에서 폭넓게 사용되고 있습니다. 베이즈의 정리가 무엇인지, 실생활에 어떻게 적용되는지 등은 여러분이 추가로 탐구해보시면 좋겠습니다. 고등학교 수학에서 이와 관련된 개념은 고등학교 <확률과 통계> 과목에서 나오는 ‘조건부확률’입니다. 앞에 나온 의료 진단 기기의 예시를 조건부확률 식을 이용해여 직접 구해보고, 이 내용을 깊이 있게 공부해보면 좋겠습니다.

홍창섭 경희여고 교사

또한 몇 년 전에는 독감백신으로 인한 사망자 수가 크게 늘어났다며 독감백신 접종에 대해 불안감이 확산된 적이 있습니다. 그때 사람들은 백신 부작용에 따른 사망을 우려했지만, 사실상 사망자가 발생하기 전 백신을 접종한 사례이므로 인과관계나 상관관계를 논하기 어려운 상황이었습니다. 이는 조건부확률의 대표적 사례이므로 이에 대해서도 심도 있게 탐구해보길 권합니다.

이처럼 확률은 일상생활에서 큰 착각을 불러일으키는 경우가 많습니다. 우리는 이 같은 오류를 범하지 않기 위해 주어진 확률을 정확하게 해석하는 능력을 갖출 필요가 있습니다.