[재미있는 수학] 상황 변화를 직관적으로 전달하죠

(41) 그래프의 기능

일차함수, 이차함수, 다항함수, 유리/무리함수, 삼각함수, 지수/로그함수, 초월함수 등 학년마다 이러한 단원을 힘들어하는 학생이 많은데, 그런 맥락에서 조금은 어깨의 힘을 풀고 편하게 받아들이며 이해해보면 어떨까 싶습니다. 다들 즐거운 수학 되세요!

Getty Images Bank

수학에서 그래프를 그리는 것과 그려진 그래프를 이해하는 것은 둘 다 매우 중요합니다. 두 과정은 마치 그리는 사람과 이해하는 사람 사이에서 이루어지는 의사소통과 같다고 할 수 있습니다. 그래프는 수학적 개념이나 상황을 시각적으로 표현한 것이므로, 상황을 빠르고 정확하게 공유하는 데 아주 유용한 도구가 됩니다.

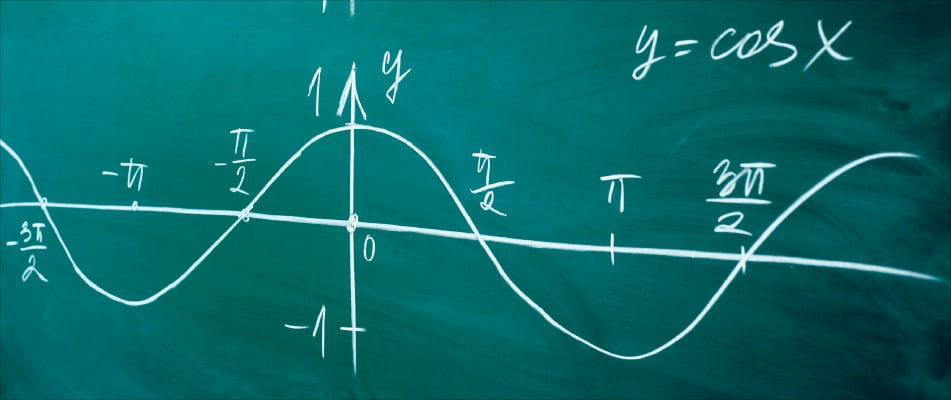
예를 들어, 큰 그릇에 물을 담는 상황을 생각해보겠습니다. 일정한 속도로 물을 담다가 중간에 더 빠른 속도로 물을 붓는다면, 이 변화 과정을 그래프로 나타낼 수 있습니다.

그런데 여기서 어떤 것을 중점으로 두고 표현하느냐에 따라 그래프의 모습이 달라질 수 있습니다. 일반적으로는 시간의 흐름에 따라 물이 차오르는 높이의 변화에 초점을 맞출 겁니다. 그렇게 되면 처음에는 우상향하는 직선의 모습으로 그려지다가 어느 순간 기울기가 큰 직선 모양으로 바뀌겠죠.

하지만 조금 특이한 경우에는 물의 높이보다 그 순간에 쏟아지는 물의 양을 기준으로 할 수도 있습니다. 이 경우 그래프는 어떻게 될까요? 앞서 말했듯 일정한 속도로 물을 담는다는 것은 순간에 쏟아지는 물의 양이 일정하다는 의미이므로, 그래프는 처음 어느 정도까지는 위로도 아래로도 움직이지 않고 평평한 모양으로 그려질 겁니다. 그러다 어느 순간 더 빠른 속도로 물을 부을 때 순간적으로 그래프는 더 위로 올라간 뒤 역시 그 지점에서 평평한 모양이 지속될 것이라고 생각할 수 있겠죠.

이를 굳이 말로 설명하지 않고 그래프로 하면 어떤 차이가 있을까요? 그래프를 그리는 사람과 보는 사람이 그래프에 대한 이해가 충분하다면 처음에 말한 대로 상황을 빠르면서도 정확하게 전달할 수 있습니다. 글로 표현하는 것에 비해 아주 뛰어난 의사소통이 되는 것이죠.

같은 상황을 두 가지 이상의 방식으로 표현할 수 있다는 점에서 수학이란 것이 하나의 표현 방식이자 언어라고 볼 수 있는 지점입니다. 한 문제에 여러 풀이 방식이 있는 것과 마찬가지인 거죠.

조금 더 확장하자면, 일정한 속도로 물을 붓는다고 하더라도 그릇의 모양에 따라 그래프가 달라질 수 있습니다. 예를 들어, 그릇이 기둥처럼 일정한 단면적을 가지고 있으면 물 높이는 일정한 속도로 증가하며 선형적 그래프가 나타납니다. 반면에 빗살무늬토기와 같이 뿔 모양으로 위쪽이 넓어지는 그릇이라면 같은 양의 물을 부어도 물 높이는 점점 느리게 올라갑니다. 이 경우 시간이 지날수록 기울기가 완만해지는 포물선 형태의 그래프가 그려집니다. 이차함수를 옆으로 뉘어놓은 것 같은 모양이 되는 거죠. 여기서 만약 그릇이 구 형태라면 어떨까요?

이처럼 특정한 상황을 다양한 방식으로 표현한 그래프는 복잡한 설명 없이도 그 상황의 변화를 직관적으로 전달해줍니다. 또 서로 다른 관점과 시각으로 상황을 이해하고 소통할 수 있도록 돕습니다. 따라서 그래프는 정확하고 빠르게 정보를 공유할 수 있는 강력한 의사소통 수단이 되는 것입니다.

그래프는 대략 그려도 충분히 효과적이지만, 정확하게 그린다면 한없이 강력해질 수 있습니다. 특히 꺾이는 점이라든지, 아래에서 위로 혹은 위에서 아래도 변화하게 되는 점 같은 부분을 정확히 아는 것을 의미합니다.

이러한 그래프는 결국 어떤 변화를 나타내는 것이고, 그러한 변화의 추이에서 유용하게 쓸 수 있는 것은 ‘최적화’된 지점이기 때문입니다. 그리고 이러한 그래프와 관련된 단원 중 종착역이라고 할 수 있는 미적분은 이것과 관련된 질문들이 중심이 되는 단원이기도 하죠.

가장 많을 때, 가장 적을 때, 가장 클 때, 가장 작을 때 등 많은 학생이 경험해본 질문들이 이러한 맥락에서 준비되고 만들어지는 것입니다. 그리고 이러한 지점을 명확히 계산하기 위해선 바로 그래프의 ‘관계식’을 알고 다루는 것이 필수입니다.

직선과 곡선에 포함된 수많은 점이 공통으로 가지는 가로 좌표와 세로 좌표 사이의 관계. 이걸 알고 다루는 것이 그래프를 보다 정확히 해석하는 열쇠인 겁니다. y는 x가 두 배 된 결과인지, x의 제곱에 세 배인 건지, 아니면 더 복잡한 관계일 수도 있겠습니다만 이 관계식을 알면 높이가 0이 되는 점은 x값이 얼마인지, 높이가 점점 줄어들다가 어느 순간부터 점점 커지기 시작하는지 제대로 분석할 수 있습니다.

이정현 푸른숲발도르프학교 교사

그래프는 일종의 표현이며 관계식과 밀접한 관계를 갖고 있습니다. 이 둘을 적절히 받아들여 표현하는 것, 그리고 다른 사람의 표현을 이해하는 것은 아주 흥미로운 작업일뿐더러 일상적으로도 유용하다는 것입니다.