#생글생글
-
학습 길잡이 기타
47. 관계사(Relatives) ③실전 문제
자~ 실전의 재미에 빠져 볼까요 ♣관계사 관련 문제들을 풀어보며 지금까지 학습한 내용을 총 점검해 보도록 하자. [1~6] 다음 문장의 [ ] 안에서 어법상 적절한 표현을 고르라. 1. Hope, [which / that] seems like the thinnest little thread, is an incredibly powerful force leading us from the most horrible problems into a...
-
시사 경제용어 따라잡기
(33) 다음 문장을 흐름에 맞게 배열해 보세요
생글생글을 휴대폰으로도 본다! 휴대폰으로 생글생글을 읽고 모바일 글쓰기를 통해 실력을 겨뤄보세요. [문제] 순서가 흩어진 다음 문장을 흐름에 맞게 배열해 보세요. ①그런데 다시 다윈이 나타나 인간을 동물의 후손으로 격하시키자 사람들은 인간만이 가진 이성에서 겨우 위안을 찾았다. ②코페르니쿠스가 인간이 우주의 중심에 있다는 믿음을 붕괴시키자 사람들은 신께서 자신의 형상을 닮은 특별한 생명체를 창조하기 위해 이 변두리 행성을 선택하셨다고 ...
-
시사 경제용어 따라잡기
8월 20일자
1.이것의 부실로 인한 미국의 신용경색 사태로 전세계 금융시장이 불안한 모습을 보이고 있다. 미국에서 신용도가 낮은 저소득층에게 일반 주택담보 대출보다 2∼4% 포인트 정도 높은 금리로 제공되는 주택자금 대출은 무엇인가? ①프라임 모기지 ②서브 프라임 모기지 ③역모기지 ④타입대 2.다음 중 적신월사(赤新月社)에 대한 설명으로 바르지 않은 것은? ①전시에는 부상자 치료, 포로 보호,평상시에는 재해 구제,보건 증진 등의 공익사업을 한다. ...
-
시사 경제용어 따라잡기
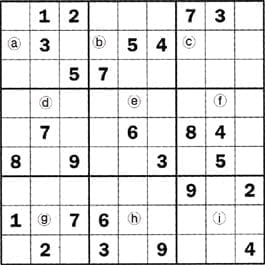
스도쿠 여행 (13)
새로운 퍼즐게임 '수학 두뇌를 키워라-스도쿠 여행' 13회 문제입니다. 방학 중 스도쿠여행의 참여 열기가 뜨거웠습니다. 스도쿠(Sudoku)는 가로와 세로 9×9의 상자 안에 1부터 9까지 숫자를 수직,수평은 물론 작은 3×3 상자 안에서도 서로 겹치지 않게 써 넣는 퍼즐게임입니다. 어느 한 곳의 숫자가 틀리면 스도쿠는 실패하게 됩니다. 스도쿠는 푸는 재미는 물론,자신도 모르게 논리적·수학적 지능을 높이는 효과도 있어 세계적으로 인기를 모으고...
-
커버스토리
여론조사와 통계 그 태생적 오류
미국의 원로 코미디언 할 로치가 자연사박물관 안내원을 소재로 웃긴 적이 있다. 어느날 한 방문객이 선사시대 공룡뼈를 구경하다 그 뼈가 얼마나 오래 전의 것인지 안내원에게 물었다. 안내원은 머뭇거리지 않고 "300만17년 됐다"고 답했다. 무슨 근거로 그렇게 정확하냐니까 안내원 왈, "내가 여기에서 처음 일을 시작했을 때 그 뼈가 300만년 됐다고 들었는데, 그 후로 나는 17년째 일하고 있다."(김진호, 통계상식 백가지) 우스갯소리로 넘기면...
-
경제 기타
남북정상회담 28~30일 평양서 개최
평화정착 기대속 대선 변수로 노무현 대통령과 김정일 북한 국방위원장의 남북 정상회담이 오는 28∼30일 평양에서 열린다고 남북 정부가 8일 공식 발표했다. 2000년 6월15일 김대중 전 대통령의 평양 방문 이후 7년여 만에 남북 정상이 다시 만나는 것이다. 정부는 이날 오전 청와대에서 백종천 청와대 안보실장,김만복 국가정보원장,이재정 통일부 장관의 공동 기자회견을 통해 이를 밝혔고,북한도 조선중앙통신을 통해 정상회담 개최 사실을 공식 발표했...
-
경제 기타
한국은행 콜금리 또 올려 外
◆한국은행 콜금리 또 올려 한국은행 금융통화위원회가 9일 콜금리 목표치를 0.25%포인트 인상,6년1개월 만에 가장 높은 연 5.0%로 끌어올렸다. 금통위는 사상 처음으로 두 달 연속 콜금리를 인상하는 초강수를 뒀다. 미국의 신용 경색과 고유가 등 불안 요인들이 상존해 있지만 경기 상승세가 기대 이상으로 강한 데다 시중의 유동성이 계속 늘어나 이같이 결정했다. 그러나 이로 인해 주택담보대출의 기준금리 역할을 하는 양도성 예금증서(CD) 유통수...
-
경제 기타
꼬리에 꼬리를 무는 학력위조와 간판사회증후군
부모님 세대의 '완소남' 알랭 들롱은 1960년 영화 '태양은 가득히'에서 야심만만한 젊은이 '리플리'를 연기했다. 리플리는 자신이 죽인 친구 행세를 함으로써 돈과 지위를 얻지만 끝내 거짓이 밝혀져 몰락한다. 그런 대담함과 대중을 속인 거짓말이 비슷해서일까. 위조된 학력을 바탕으로 큐레이터로서는 최고 지위라 할 수 있는 광주비엔날레 예술감독까지 올랐다가 졸지에 나락으로 떨어진 신정아 전 동국대 교수도 리플리에 비유될 수 있다. 그리고 또 다른...