[재미있는 수학] 모든 도형의 기본…각 알면 천문학적 길이도 잴 수 있어

(14) 삼각함수가 중요한 이유

삼각형의 닮음 조건 중 AA닮음은 의외로 강력한 조건입니다. 두 개의 각만 같다면, 작은 삼각형의 길이를 이용해 천문학적인 길이를 앉은 자리에서 종이와 연필만 가지고도 추론해 낼 수 있기 때문입니다.

Getty Images Bank

수학 교과서는 난도와 위계를 따져 단원을 구분합니다. 이 중 많은 학생이 어려워하는 단원을 꼽자면 삼각함수가 아닐까 생각합니다. 이번에는 삼각함수의 도입 부분에서 교과서와 문제집에는 생략된 흥미로운 맥락을 살펴볼까 합니다.

먼저 생각해볼 것은 ‘왜 삼각형인가’입니다. 삼각형은 중·고등학교 기하학에서 큰 비중을 차지합니다. 그 이유는 단순합니다. 모든 다각형은 대각선을 만들어 삼각형으로 쪼갤 수 있기 때문입니다. 삼각형을 안다는 것은 모든 도형을 안다는 말과 다르지 않기에 합동, 닮음, 피타고라스의 정리, 삼각비, 삼각함수 등 많은 단원이 삼각형과 관련되어 있는 것입니다.

이어서 생각해볼 것은 삼각비, 삼각함수의 등장 배경입니다. 그 바탕에는 삼각형의 닮음이 있습니다. 두 삼각형이 닮기 위해서는 세 가지 조건이 필요합니다. 그중 AA닮음은 의외로 강력한 조건입니다. 두 개의 각만 같다면, 작은 삼각형의 길이를 이용해 천문학적인 길이를 앉은 자리에서 종이와 연필만 가지고도 추론해낼 수 있기 때문입니다. 별 생각 없이 푼 문제 중 하늘에 떠 있는 비행기의 높이, 두 섬 사이의 거리처럼 직접 재는 것이 거의 불가능한 대상을 종이 위에 각이 같은 삼각형을 그려냄으로써 손쉽게 근삿값을 구할 수 있습니다.

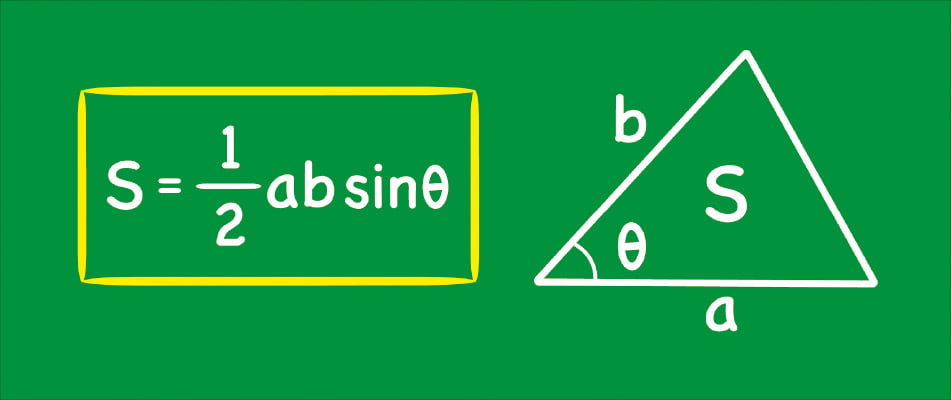
직각삼각형으로 한정한다면 한 각만으로도 삼각형 길이의 비를 알아내 실제 길이를 파악할 수 있습니다. 더 나아가 삼각형으로 쪼개진 수많은 다각형도 유한번의 계산을 통해 (이론적으로는) 완벽하게 알 수 있습니다. 그래서 비율을 정확하게 계산해놓는 것이 중요한 일이 되었습니다. 이것이 바로 빗변과 높이의 길이의 비(sin), 빗변과 밑변의 길이의 비(cos), 밑변과 높이의 길이의 비(tan)에 별도의 이름을 주고 그 값과 그 자체의 성질에 주목하게 되는 과정의 시작인 것입니다.

자연스럽게, sin의 값을 그래프로 표현하고자 하는 시도를 하게 됩니다. x축을 각의 크기로 하고 y축을 sin의 크기로 한다면 각이 점점 커지면서 sin이 어떻게 변하는지 알 수 있게 됩니다. 그렇다면 삼각함수가 가지는 여러 특성을 연구하고 이용할 수 있겠죠. 하지만 이러한 시도는 두 개의 문제를 지니게 됩니다.

그중 첫 번째는 각의 양적 한계입니다. 삼각함수를 배우기 전까지 각은 0°에서 360°까지만 존재하며, 의미를 가집니다. 그런데 x축에 각의 크기를 대응시키자니 정의역이 너무 좁고 유한해 삼각함수가 가지는 성질을 표현하기에 부족합니다. 따라서 동경이라는 개념을 도입해 사용하게 됩니다. 즉 “90°와 450°는 서로 다른 각임은 확실하나, 다만 그 각을 나타내는 동경은 같은 위치에 있다”는 개념을 도입하게 되는 거죠. 비록 본질적으로 달라지는 것은 없으나 이 과정을 통해 각은 -∞에서 +∞까지의 값을 가질 수 있도록 확장됩니다.

그런 뒤에 정신을 차리고 삼각함수로 돌아와 보면 상당한 문제가 있는 상황을 마주하게 되죠. sin(-300°)이나 sin(1200°)처럼 기존 직각삼각형의 이미지로는 도저히 설명할 수 없는 표현을 설명해야 합니다. 그렇기에 삼각함수는 이 지점에서 삼각형이라는 기하학적 한계를 벗어나고, 좌표평면 위의 한 점과 그 동경을 사용해 다시 정의되는 과정을 거치는 것입니다. 어떻게 정의하는지는 교과서에서 찾아볼 수 있으나 그 배경에는 이러한 흐름과 목적, 당위성, 아이디어가 있는 것입니다.

마지막은 각의 질적인 문제 해결입니다. x축 위에 90°를 어떤 수에 대응시켜 그래프를 그릴 것이냐는 문제입니다. 어떻게 보면 기존에 사용하는 육십분법의 한계라고도 볼 수 있습니다. 그저 한 바퀴를 360으로 나누었을 뿐이며, 360이어야 할 이유도 수학적 당위성이 없는 것이기 때문입니다. 따라서 수직선상의 길이 ‘1’과 새로운 각도 단위 ‘1’을 같은 비율로 취급할 수 있는 새로운 각도의 단위가 필요합니다.

이 방법이 바로 삼각함수 단원 앞부분에서 배우는 호도법입니다. 중학교 3학년에서 원주각을 배울 때 우리는 ‘중심각의 크기와 호의 길이는 비례한다’는 사실을 배웁니다. 이 사실에 주목했을 때, 중심각이 1이고 호의 길이가 1이라면 어떤 일이 벌어질까요? 두 변수는 비례하기에, 중심각이 t일 때 호의 길이도 t가 됩니다. 즉 각의 크기와 선분의 길이를, 단위를 별도로 표기하지 않더라도 혼용해서 사용해도 된다는 것이죠. 참으로 아름다운 아이디어와 결론 아닙니까.

삼각함수는 어려운 단원입니다. 특히 앞부분에서 일반각과 호도법, 삼각함수의 정의에 대한 내용이 다소 뜬금없다고 느껴질 수 있습니다. 하지만 이러한 흐름을 이해하며 따라가다 보면 어느새 하나하나의 아이디어가 대단하고 의미 있게 보일 것입니다.

이정현 푸른숲발도르프학교 교사