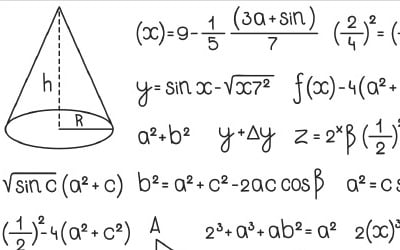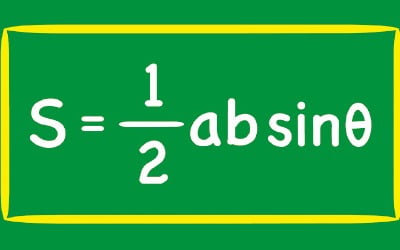생글생글

학습 길잡이 기타

천체 움직임 설명 위해 삼각함수 등장

삼각비와 삼각함수 중 어떤 개념이 먼저 발견되었을까요? 먼저 삼각비는 고대 그리스에서 시작된 개념으로, 기하학에서 삼각형의 각과 변의 관계를 설명하기 위해 사용되었습니다. 고대 그리스의 수학자들은 직각삼각형에서 각도와 변의 비율을 계산하는 방법을 연구했으며, 이를 바탕으로 삼각비 개념이 발전했습니다. 예를 들어, 피타고라스는 직각삼각형의 변 사이 관계를 설명하는 ‘피타고라스 정리’를 세웠고, 이는 삼각비의 기초적 아이디어와도 연결됩니다. 반면 삼각함수는 훨씬 후대에 나타난 개념입니다. 삼각비를 체계화한 후, 19세기에 들어서야 삼각함수가 등장하게 됩니다.그리스-로마 시대부터 수학자들은 다양한 도형을 기본 삼각형으로 나누어 분석했고, 특히 삼각형의 세 변 길이의 비율에 큰 관심을 가졌습니다. 이를 보다 정확히 파악하기 위해 등장한 것이 바로 삼각비입니다. 삼각비는 직각삼각형에서 정의되며, 그 핵심은 각도와 변의 길이 사이 관계를 설명하는 데 있습니다. 삼각비의 기본은 직각삼각형에서 시작하며, 사인(sin), 코사인(cos), 탄젠트(tan)라는 세 가지 중요한 개념으로 정리합니다.먼저 sin은 직각삼각형에서 주어진 각의 대변의 길이를 빗변의 길이로 나눈 값을 의미합니다. 반대로 cos은 주어진 각의 인접변의 길이를 빗변의 길이로 나눈 값입니다. 마지막으로 tan는 주어진 각의 대변의 길이를 인접변의 길이로 나눈 비율로 정의합니다. 이 세 가지 삼각비는 직각삼각형에서 각과 변의 관계를 설명하는 가장 중요한 도구로, 고대 수학자들이 삼각형의 특성을 분석하는 데 필수적 역할을 했습니다.이렇게 직각삼각형에서 정의한 삼각비는 다양한 기하학적 문제

학습 길잡이 기타

모든 도형의 기본…각 알면 천문학적 길이도 잴 수 있어

수학 교과서는 난도와 위계를 따져 단원을 구분합니다. 이 중 많은 학생이 어려워하는 단원을 꼽자면 삼각함수가 아닐까 생각합니다. 이번에는 삼각함수의 도입 부분에서 교과서와 문제집에는 생략된 흥미로운 맥락을 살펴볼까 합니다.먼저 생각해볼 것은 ‘왜 삼각형인가’입니다. 삼각형은 중·고등학교 기하학에서 큰 비중을 차지합니다. 그 이유는 단순합니다. 모든 다각형은 대각선을 만들어 삼각형으로 쪼갤 수 있기 때문입니다. 삼각형을 안다는 것은 모든 도형을 안다는 말과 다르지 않기에 합동, 닮음, 피타고라스의 정리, 삼각비, 삼각함수 등 많은 단원이 삼각형과 관련되어 있는 것입니다.이어서 생각해볼 것은 삼각비, 삼각함수의 등장 배경입니다. 그 바탕에는 삼각형의 닮음이 있습니다. 두 삼각형이 닮기 위해서는 세 가지 조건이 필요합니다. 그중 AA닮음은 의외로 강력한 조건입니다. 두 개의 각만 같다면, 작은 삼각형의 길이를 이용해 천문학적인 길이를 앉은 자리에서 종이와 연필만 가지고도 추론해낼 수 있기 때문입니다. 별 생각 없이 푼 문제 중 하늘에 떠 있는 비행기의 높이, 두 섬 사이의 거리처럼 직접 재는 것이 거의 불가능한 대상을 종이 위에 각이 같은 삼각형을 그려냄으로써 손쉽게 근삿값을 구할 수 있습니다.직각삼각형으로 한정한다면 한 각만으로도 삼각형 길이의 비를 알아내 실제 길이를 파악할 수 있습니다. 더 나아가 삼각형으로 쪼개진 수많은 다각형도 유한번의 계산을 통해 (이론적으로는) 완벽하게 알 수 있습니다. 그래서 비율을 정확하게 계산해놓는 것이 중요한 일이 되었습니다. 이것이 바로 빗변과 높이의 길이의 비(sin), 빗변과 밑변의 길이의 비(c