[신철수 쌤의 국어 지문 읽기] 난해한 함수 관계, 국어 능력 신장을 위해 넘어야 할 산!

슬기로운 국어 학습

(6) 함수의 다양한 유형 이해

기업 입장에서 한계비용은 상품 생산량을 한 단위 증가시키는 데 추가로 드는 비용이며, 한계수입은 상품을 한 단위 더 생산해 판매할 때 추가로 얻는 수입이다. 완전경쟁시장에 있는 기업이라면 상품의 시장 가격 그 자체가 한계수입이 된다. <중략> 기업이나 소비자는 시장에서 결정된 상품 가격을 주어진 것으로 받아들이며 이 가격이 기업의 한계수입이 된다. 상품을 사려는 사람들이 많아져 시장 수요가 증가해 상품 가격이 오른다면, 한계수입도 그만큼 동일하게 오른다.

생산을 계속할 때 손실이 발생하는 상황이 아니라면, 기업은 한계비용과 한계수입이 일치하도록 생산량을 조절해 이윤을 극대화할 수 있다. 한계비용이 한계수입보다 큰 경우에는 상품 생산량을 한 단위 더 줄일 때 그로 인해 추가로 절약되는 비용이 줄어들 수입보다 크므로 생산량을 줄여 이윤을 증가시킬 수 있다. 이와 반대로 한계수입이 한계비용보다 큰 경우에는 생산량을 늘려 이윤을 증가시킬 수 있다. <중략>

이 기업은 평균비용을 상품의 시장 가격과 비교해 보고 만약 가격이 평균비용곡선의 최저점에도 미치지 못한다면, 생산량이 얼마이든 그 가격에 상품을 판매해 봤자 손실을 피할 수 없다고 판단할 것이다. 그렇다면 투입된 총비용을 전부 회수해 손실 발생을 막는 것이 이 기업에 합리적인 결정일 수 있다.

2020학년도 09월 교육청 전국연합평가

…을 한 단위 증가시키는 데 추가로 드는 …을 한 단위 더 …할 때 추가로 얻는함수는 수학에서 다루는 개념이다. 그런데 우리는 일상생활에서 ‘국어를 잘하고 싶어? 그럼 책을 많이 읽어. 책을 많이 읽을수록 국어를 잘하게 돼’라고 말한다. 이는 ‘읽는 시간’을 독립 변수로 하고, ‘국어 능력’을 종속 변수로 하는 함수이다. 따라서 함수는 수학 외에도 여러 분야의 글에 등장하며, 그것을 읽어 내는 능력 역시 국어 능력이다.

경제학에서는 ‘단위’라는 말을 즐겨 쓴다. 이는 ‘빵 1개’ ‘옷 1벌’ ‘차 1대’ 등과 같이 ‘개, 벌, 대’라는 말로 정해서 말하기 어렵기 때문에 그것들을 통칭해서 쓰는 것이다. 일상생활에서는 낯선 어휘이므로 경제 관련 글을 잘 읽고 싶다면 익숙해져야 한다.

‘증가’ ‘추가’는 함수임을 단적으로 떠올리게 하는 어휘다. 보통 함수임을 나타내는 어구는 ‘Aㄹ 때 B’, ‘A면 B’, ‘A는 데 B’, ‘A어(여) B’와 같은 형태로 나타난다. 따라서 여기에서는 ‘상품 생산량’이 독립변수, ‘비용’이 종속변수인 함수와 ‘상품 판매(량)’이 독립변수, ‘수입’이 종속변수인 함수, 그리고 ‘사람(수)-시장 수요-상품 가격-한계수입’ 사이의 함수 등을 볼 수 있다. 상품 가격이 오른다면, 한계수입도 그만큼 동일하게 오른다. … 생산을 …할 때 손실…이 발생

함수하면 자동적으로 떠올려야 하는 것이 ‘(정)비례’, ‘반비례’이다. 앞에서 ‘증가-들다’, ‘더-얻다’, ‘많다-증가’라는 말을 음미해 보자. 이것들은 이 함수들이 모두 비례 관계임을 보여주는 것이다. ‘상품 가격 오름-한계수입 오름’도 역시 비례 관계임을 보여준다. 그에 비해 ‘손실…이 발생’은 수입 감소이므로, ‘생산 (증가)-수입 감소’는 반비례 관계임을 보여준다.

한편 ‘그만큼 동일하게’라는 말은 좀 더 심오한 사고가 필요하다. 이에 대한 이해는 그래프를 통해 하는 것이 좋다. B와 같은 직선 그래프는 x축이 1, 2 등으로 변할 때 y축은 b, c로 변하는데 그 비율이 같다. 그러나 A와 같은 곡선 그래프는 x축이 1, 2 등으로 변할 때 y축은 a, c로 변하는데 그 비율이 다르다. ‘그만큼 동일하게’는 B와 같은 그래프를 떠올리게 만드는 어구이다. 이 세상에는 A와 B 그래프 외에도 수많은 모양의 그래프로 표현되는 함수가 있다. 각각의 그래프를 떠올리게 하는 어구는 그 수보다 더 많으니 각각의 어구들을 이해해야 한다. 한계비용이 한계수입보다 큰 경우에는 … 생산량을 줄여 … 이와 반대로 한계수입이 한계비용보다 큰 경우에는 … 생산량을 늘려우리는 수많은 선택을 한다. 선택할 때는 기준이 있다. 그 기준에 맞으면 선택을 하고, 맞지 않으면 선택을 하지 않는다. 따라서 기준과 선택 결과는 수없이 많은 글에 등장하며, 그것을 읽어내는 연습이 필요하다. ‘Aㄹ 경우(ㄹ 때) B이다. 이와 반대로 A 아닐 경우(때) B 아니다’라는 문장은 기준과 선택 결과를 의식하며 읽어야 하는 대표적인 사례다. A는 선택을 위한 기준이 되며, B는 선택 결과이다. 여기에서는 ‘한계비용’, ‘한계수입’의 관계가 기준이 되고 있다. 즉 ‘한계비용>한계수입’과 ‘한계비용<한계수입’이 기준인 것이다. ‘생산량을 늘림’, ‘생산량을 줄임’은 선택 결과이다. ‘한계비용=한계수입’인 경우도 있지만, 여기에서는 그에 따른 선택 결과에 대해 언급하고 있지 않다. 이는 순서도를 그려가면서 연습을 하면 좀 더 쉽게 이해할 수 있다.

가격이 평균비용곡선의 최저점에도 미치지 못한다면 … 손실

경제학에서 가장 기본이 되는 개념은 ‘(상품) 가격’이다. 생산과 소비는 가격이라는 것에 의해 결정된다. 가격이 생산하는 비용보다 낮으면 손해이고, 높으면 이익이다. 이 정도는 일상생활에서도 쉽게 겪을 수 있는 것이니 이해하기는 쉽다.

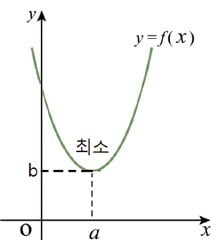
그런데 여기에서는 ‘평균비용곡선의 최저점’이라는 개념 때문에 그 내용이 쉽게 이해되지 않는다. 함수의 본질이 ‘변화’라는 것을 이해해야 하기 때문이다. ‘곡선’이라는 말에서 비용이 수없이 변한다는 것과 ‘최저점’이라는 말에서 변화 중에서 가장 낮은 것이 있다는 것을 떠올려야 한다. 이것을 또다시 그래프로 이해하면 도움이 된다. 앞에서 말한 B와 같은 곡선 그래프 말고도 <그림1>과 같은 곡선 그래프도 있다. x 축이 a일 때, y축이 b인데, 만약 여기에서의 내용이라면 a인 경우 비용이 최소, 즉 최저가 된다는 것이다. 아마 학생들은 여기에서도 함수의 본질을 알아 두는 것이 국어 능력 향상에 얼마나 중요한지를 느낄 수 있을 것이다.

여기에서는 선택과 기준에 대한 이해도 필요함을 느낄 수 있다. 즉 ‘가격<최저 비용’, ‘가격>최저 비용’에 따라 선택 결과가 달라진다는 것을 알 수 있어야 한다는 것이다. 이는 순서도를 활용하면 이해에 도움이 될 것이다.

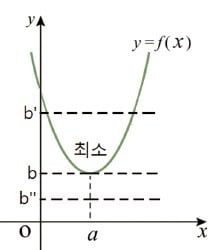
한편 가격도 변한다는 것은 상식이다. 그러므로 이를 이용해 그래프를 변형하는 임기응변이 있다면 국어 능력이 우수하다고 할 수 있다. 즉 <그림2> 그래프와 같이 가격 b에서 b′ 또는 b″로의 변화는 가격이 오르고 내림을 보여준다. 그렇다면 최저점은 가격의 아래에 있거나, 위에 있게 되는 변화를 하게 된다. 이 또한 ‘변화’에 따라 판단도 달라진다는 것을 염두에 두고 읽는 것이 필요함을 보여준다. ☞ 포인트

성보고 교사

① 함수와 관련한 어구, 판단 기준과 판단 결과를 보여주는 어구가 어떤 것들인지 알아 두자.

② 함수 관계에서 (정)비례, 반비례 관계를 파악하는 습관을 들이자.

③ 함수 관계는 그래프를 떠올리며 읽는 연습을 많이 하자.

④ 다양한 그래프들을 떠올리게 하는 어구들이 있음을 기억하자.

⑤ 함수의 본질은 ‘변화’이며 곡선으로 표현되는 함수에는 최저점이 있음을 알아 두자.

_{※여기에 제시된 그림들은 글의 내용을 바탕으로 한 것으로 실제 사실과 다를 수 있습니다.}