[재미있는 수학] 같아 보이는 상황, 수학으로 풀어보면 차이 알 수 있어

(25) 합성함수

겉으로 보기에 같아 보이는 상황을 자세히 알아보면 서로 다른 것들이 있을 수 있는데, 이를 밝히는 데에 수학이 유용하게 사용될 수 있습니다. 그리고 학교에서 배우는 수학 내용을 실생활과 연결지어 생각해 보면 수학에 대한 관심과 흥미가 더욱더 생길 것입니다.

Getty Images Bank

중국 송나라 때 이야기입니다. 어떤 사람이 원숭이에게 도토리를 아침에 세 개 주고 저녁에 네 개 주겠다고 하니 원숭이들이 먹이가 적다고 화를 내다가 그래서 아침에 네 개 주고 저녁에 세 개 주겠다고 하니 좋아했다고 합니다. 이 이야기에서 유래된 ‘조삼모사(朝三暮四)’라는 말은 ‘아침에 세 개, 저녁에 네 개’라는 뜻으로, 당장 눈앞에 나타나는 차이만을 알고 그 결과가 같음을 모르는 어리석음을 비유한 말입니다.

이를 수학으로 나타내면 아침에 세 개, 저녁에 네 개는 3+4=7이고, 아침에 네 개, 저녁에 세 개는 4+3=7이므로 두 값이 같습니다. 이는 두 수의 덧셈에서 두 수의 순서를 바꾸어 더해도 결과가 같다는, 즉 덧셈의 교환법칙이 성립함을 말합니다. 원숭이가 덧셈의 교환법칙이 성립함을 알았다면 조삼모사 같은 이야기는 없었을 것 같습니다.

그러면 다음 상황은 어떨까요?

다음과 같이 두 스포츠센터의 광고지가 있습니다. 할인하기 전 두 스포츠센터의 1년 등록 비용은 같고, 이번 달 안에 1년 등록하려고 합니다. 두 스포츠센터 중에서 어느 곳을 선택해야 등록 비용이 적게 들까요?

앞의 조삼모사 이야기를 생각해보면 두 센터의 등록 비용은 같을 것 같습니다. 그런데 과연 두 센터의 등록 비용이 같을까요? 이는 사실 예를 들어 생각해보면 금방 알 수 있습니다. 할인하기 전 스포츠센터의 등록 비용을 30만원이라고 하면, A 스포츠센터의 경우 30만원에서 20% 할인한 후 5만원이 추가 할인되므로 등록 비용은 300000×0.8-50000=190000(원), B 스포츠센터의 경우 30만원에서 5만원을 할인한 후 20% 추가 할인되므로 등록 비용은 (300000-50000)×0.8=200000(원)입니다. 따라서 이 예를 보면 B 스포츠센터보다 A 스포츠센터의 등록 비용이 더 적게 든다는 것을 알 수 있습니다.

앞의 조삼모사 사례에서는 계산 순서를 바꾸어도 결과가 같았는데, 이 사례에서는 왜 결과가 다를까요? 이를 수학적으로 알아봅시다. 이는 함수로 생각할 수 있습니다.

할인하기 전 스포츠센터의 등록 비용이 x원일 때, 20% 할인한 비용을 f(x)원, 5만원 할인한 비용을 g(x)원이라고 하면, f(x)=0.8x, g(x)=x-50000입니다.

20% 할인, 5만 원 추가 할인 순서로 적용한 비용은 f(x)를 먼저, g(x)를 나중에 계산하므로 (gf)(x)입니다. 이를 계산하면 (gf)(x)=g(f(x))=g(0.8x)=0.8x-50000입니다.

5만 원 할인, 20% 추가 할인 순서로 적용한 비용은 g(x)를 먼저, f(x)를 나중에 계산하므로 (fg)(x)입니다. 이를 계산하면 (fg)(x)=f(g(x))=f(x-50000)=0.8x-40000입니다. 따라서 (gf)(x)=0.8x-50000, (fg)(x)=0.8x-40000이므로 값이 서로 다르다는 것을 알 수 있고, B 스포츠센터보다 A 스포츠센터의 등록 비용이 더 적게 든다는 것도 다시 한번 확인할 수 있습니다.

이렇게 스포츠 센터 등록 비용의 이야기처럼, 겉으로 보기에는 같아 보이는 것도 내용을 자세히 알아보면 서로 다른 것이 있습니다. 그리고 그 이유를 밝히는 데 수학이 사용될 수 있음을 확인했습니다.

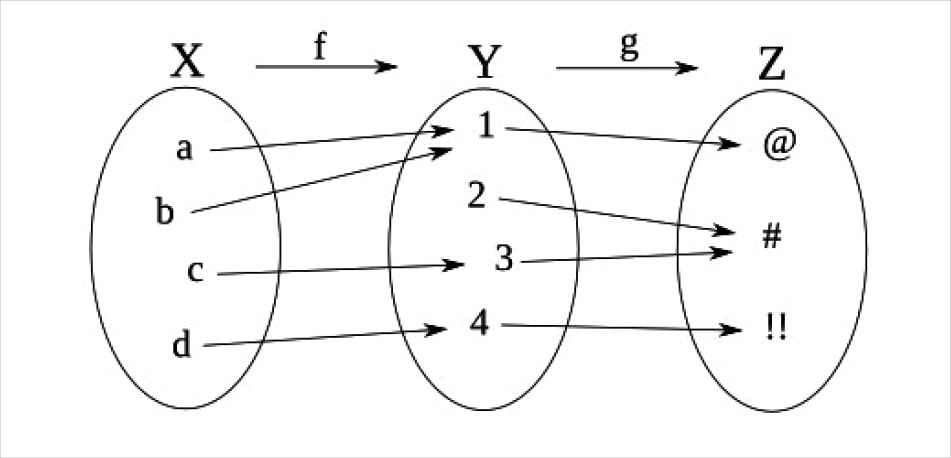
(gf)(x), (fg)(x)와 같은 것을 합성함수라고 합니다. 앞에서 확인한 것처럼 일반적으로 합성함수에서는 교환법칙이 성립하지 않습니다.

홍창섭 경희여고 교사

합성함수에 대한 내용은 고등학교 1학년 수학의 ‘함수’ 단원에서 배웁니다. 합성함수는 일반적으로 교환법칙이 성립하지 않는다는 것을 학교에서 강의하면 학생들이 그 의미를 이해하지 못하는 경우가 많습니다. 그런데 앞의 사례와 같이 실생활과 연결 지어 보니까 어떤가요? 재미있지 않았나요? 그리고 이런 함수를 실생활에서 유용하게 사용할 수 있겠다는 생각이 들 것입니다. 수학에 대한 관심과 흥미를 높이기 위해 학교에서 배우는 내용을 실생활과 연결 짓는 습관을 길러보길 바랍니다.