생글생글

gear up · step on it · open up throttle 등…영어에는 자동차 부품을 활용한 표현이 많아요

Golfzon County Co. is gearing up for an initial public offering, which will offer MBK Partners a chance to exit from its investment in South Korea’s largest golf course operator with decent returns. Golfzon County on Friday submitted its appli...

"정부, 밤새워 일한다고 경제성장 안된다"…"민간 경제로 창의적·질적인 성장 해야"

이창용 신임 한국은행 총재가 어제 취임사에서 ‘민간 주도 경제 성장’을 특별히 강조했다. 이 총재는 “디지털 경제 전환, 지정학적 경제 블록화 등으로 한국 경제는 대전환의 갈림길에 섰다”며 “우리 경제가 올바른 선택을 하기 위해 경제정책의 프레임을 과감히 바꿔야 한다”고 밝혔다. 구체적으로 “과거와 같이 정부가 산업정책을 짜고 모두가 밤새워 일한다고 경제 성장을 기대할 ...

주주로 권리를 행사하는 보통주와 달리 의결권 없는 우선주는 배당 더 많이 받아요

경제신문 기사를 읽을 때 종종 OO주라는 별명이 붙은 주식 종목을 발견하곤 합니다. 배당주 가치주 우선주 등 종류도 다양합니다. 이 중 우선주는 특이하게 ‘별명’이 기업 이름 뒤에 붙습니다. ‘삼성전자’라는 종목이 있는데 ‘삼성전자우’라는 종목이 따로 있는 것처럼 말입니다. 여기서 삼성전자는 보통주, ‘우’라는 글자가 뒤에 붙은 삼성전자우는 우선주라고 말합니...

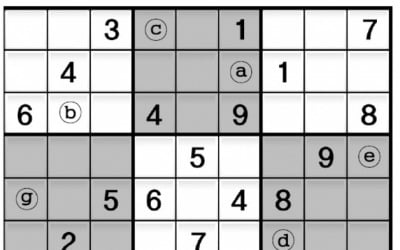
스도쿠 여행 (632)

VR 헤드셋만 쓰면 나도 세상도 원하는 대로…실감나는 메타버스, 가상이 일상 된 현실

2045년, 지구는 식량 파동으로 황폐하게 변했고 경제 기반은 무너진 지 오래다. 영화 ‘레디 플레이어 원’의 주인공 웨이드는 2025년 태어난 자기 또래를 ‘사라진 세대’라고 부른다. 암울한 현실에서 벗어나 가상현실(VR) 게임인 ‘오아시스’에 접속해 살아가기 때문이다. VR 헤드셋을 쓴 채 오아시스에 접속하는 순간 누구든 바라던 모습으로 원하는 일을 할 수 있다. 웨이드는 오아...

3학년 1학기까지 반영되는 생활기록부 점검하세요

수시 전형을 준비하는 고등학교 3학년 학생의 경우 3학년 1학기에 해당하는 생활기록부 내용까지가 대입 전형의 평가 자료로 활용됩니다. 달리 말하면 생기부를 개선할 수 있는 활동을 할 시간은 지금이 유일하다는 것입니다. 자신의 강점을 보강하고, 약점을 보완하려면 어떻게 해야 할까요. 첫 번째로 자신의 생기부를 돌아봐야 합니다. 생기부에서 드러낼 수 있는 역량은 크게 교과 역량과 교과 외 학업 역량, 인성 역량이 있습니다. 교과 역량은 학생이 주...

오늘 주인공은 어린이

초·중생용 경제·논술신문 ‘주니어 생글생글’의 이번 주 커버 스토리 주제는 어린이입니다. 위인들의 성장 과정을 살펴보면서 그들에게도 저마다 꿈을 키운 어린 시절이 있었음을 강조했습니다. 또 어린이날을 만들고 어린이의 권리에 대해 고민한 소파 방정환 선생의 이야기를 담았습니다. 이 밖에 숙박 공유 업체 에어비앤비를 창업한 세 청년, 브라이언 체스키와 조 게비아, 네이선 블레차르지크의 성공 스토리도 실...

함수는 요술 항아리! 어떤 함수식으로 된 항아리지?

‘우리글’이라는 검색어를 … 18글자의 대상 문자열에서 검색한다고 가정해 보자. 가장 간단히 떠올릴 수 있는 방법은 ‘우리글’이 3글자이므로 대상 문자열을 3글자씩 잘라 1글자씩 비교하는 것이다. … 하나의 비교 대상을 확인하기 위해서는 3글자를 각각 비교해야 하므로 총 16×3번 비교를 하게 될 것이다. 검색어와 비교 대상을 … 3글자씩 한 번에 비교...