-
진학 길잡이 기타
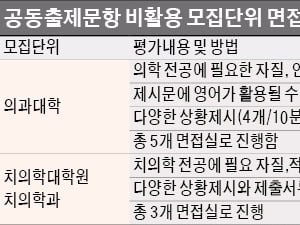
대입 실전면접…학과별 학생부중심 질문군
Ⅰ. 들어가며 최근 학생부종합전형, 학생부교과전형, 특기자전형 등 수시 면접이 시행되고 있다. 학교생활기록부를 바탕으로 학생마다 대학의 전공 공부를 잘할 수 있는지 확인하는 질문이다. 그렇다고 전공에 대한 지식이나 구체적인 교과지식을 직접적으로 물어보지는 않는다. 하지만 제출한 자기소개서의 진위를 확인한다는 취지에서 다양한 질문을 하게 된다. 학생들의 답변 모습 속에서 학업에 대한 열정과 전공 공부 및 미래에 대한 명확한 비전을 확인하고자 하...
-
학습 길잡이 기타
최준원의 자연계 논술 노트 (281)
-
진로 길잡이 기타
100문제로 직무수행·직업기초 모두 평가
금융NCS시험을 준비하는 응시자들에겐 많은 공부량이 큰 부담이 되는 게 사실이다. 인력을 채용하는 은행 등이 국가직무능력표준(NCS)에 따라 직무수행능력과 직업기초능력 두 가지를 모두 요구하기 때문이다. 은행 취업을 준비하는 응시자들로선 이들 두 가지 평가를 모두 준비할 수밖에 없다. 11월12일 서울 부산 대전에서 치러질 제2회 한경금융NCS 시험이 직무수행능력과 직업기초능력 평가 문제를 모두 담은 것은 응시자들이 시험 한 번으로 이들 두 가...
-
진로 길잡이 기타
민간자격1호 한경금융NCS 제2회 시험 준비하는 교사 2인
전국 특성화고교들이 ‘민간자격 1호 금융NCS 시험’인 ‘한경금융NCS’ 제2회 시험 준비에 한창이다. 이미 서울여상 등 10여개 특성화고가 단체 응시 접수를 마쳤다. 단체 응시를 준비 중인 이장배 충주상업고 취업담당 교사와 조송이 광신정보산업고 교사를 만났다. “내년 응시자 크게 늘 것…미리 자격 따야” 이장배 충주상고 교사 “은행을 비롯한 금융회사들...
-
홍성호 기자의 열려라 우리말
홍성호 기자의 열려라! 우리말 - 배시원 쌤의 신나는 영어여행
맞춤법 공략하기 (16) - '등쌀'과 '등살'의 구별 지난 호에서 우리 맞춤법을 관통하는 양대 원칙, 즉 ‘소리적기’와 ‘형태적기’에 대해 살펴봤다. 수많은 단어 표기를 일일이 외우는 것은 불가능할뿐더러 비효율적인 일이다. 요즘은 인터넷과 모바일이 발달해 정확한 단어 표기도 금세 찾아 볼 수 있다. 글을 쓰다가 표기가 헷갈릴 때 간단히 찾아볼 수 있는 여건이 갖춰진 것이...
-
학습 길잡이 기타
그곳의 돼지가 모두 흰 것을 보고 부끄러워하고 돌아갔다. - 동관한기
▶후한 광무제 때 일이다. 팽총은 평소 감정이 좋지 않았던 주부(朱浮)를 치기 위해 군사를 일으켰다. 주부는 팽총에게 글을 보내 꾸짖는다. “그대는 스스로를 자랑하며 자신의 공(功)이 천하에 높다고 여긴다. 옛날 요동에서 머리가 흰 새끼 돼지가 태어나자 기이하게 여겨 황제에게 바치려고 했다. 하지만 하동에 이르렀을 때, 그곳의 돼지가 모두 흰 것을 보고 부끄러워서 다시 돌아갔다고 한다. 만일 그대의 공을 조정에서 논한다면 저 요동의 ...
-
경제 기타
고대 종교의식에서 출발한 축제문화 지역경제 활성화시키는 알짜로 발전
청량한 가을 날씨가 한창인 요즘에는 여기저기서 크고 작은 축제가 많이 열리곤 한다. 지역별로 전통적이고 특색 있는 축제부터, 젊은이들의 트렌드를 반영한 음악, 토크, 예술 등 문화를 선도하는 축제 등 다양한 종류의 축제들이 개최돼 가을 특유의 상쾌함 속에 훈훈한 열기와 흥을 더한다.최근 국내에는 불꽃축제나 여러 종류의 음악 페스티벌 등 인기 있는 축제가 많고, 축제문화가 활발하게 형성되고 있는데, 축제는 아주 오래전부터 역사적으로 그 유래가 매...
-
진학 길잡이 기타
수시·정시 당락 열쇠 '수능'에 전력투구해야…수능이후 대학별고사도 주 1회 미리 준비를
2017학년도 대학수학능력시험(11월17일 목)이 이제 얼마 남지 않았다. 올해 수능 응시자는 지난해 63만 1187명보다 2만 5000여명 줄어든 60만 5988명이다. 이중 재학생이 전체의 약 76%인 45만 9000여명, 재수생 및 검정고시생은 14만 6000여명이다. 작년과 마찬가지로 올해도 대다수 대학들이 수시모집에서 추가 합격을 실시하고 등록 여부에 관계없이 추가합격자로 선발되면 정시지원이 금지되는 점에 유의하자. 정시모집에서는 전체...