-
대입 전략
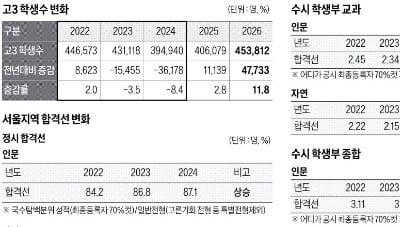
올해 고3 학생수, 12% 늘어 45만3812명…경쟁률·합격선, N수생 변수따라 크게 달라질 듯
2026학년도 고3 학생 수는 45만3812명이다. 직전 연도에 비해 4만7733명, 11.8%가 늘어난 수치다. 소위 2007년생인 황금 돼지띠의 해에 태어난 학생들이 금년도 고3 학생이 된다. 통합수능이 도입된 2022학년도 이후 가장 많다.학생 수가 늘어 2026학년도 대학입시는 치열한 경쟁과 함께 합격 점수도 올라갈 것이라고 쉽게 전망할 수 있다. 수험생들은 다소 불안해할 수도 있다. 하지만 예상과 달리 경쟁률이 줄고 합격 점수가 낮아질 수도 있다.2022학년도 44만6573명, 2023학년도 43만1118명, 2024학년도 39만4940명으로 고3 학생 수는 연속 감소해왔다. 2022학년도와 2024학년도 두 개 연도만 놓고 비교할 때 학생 수는 5만1633명으로 급격히 줄어들었다.학생 수가 큰 폭으로 줄어 당연히 입시 경쟁이 완화되고, 합격 점수도 낮아질 것으로 예상했지만 2022학년도부터 2024학년도까지 대학에서 공식 발표하는 대학알리미 합격 점수는 이러한 학생 수 변화에 따른 예상과 다르게 나타났다.대학알리미 발표 기준으로 서울권 인문계 정시 합격 평균 점수는 국수탐 백분위 평균 점수 기준 2022학년도 84.2점, 2023학년도 86.8점, 2024학년도 87.1점으로 상승했다. 2024학년도는 2022학년도에 비해 무려 2.9점 상승했다. 학생 수가 5만1633명이나 줄었음에도 합격 점수는 크게 상승한 것이다.서울권 자연계 정시 합격 점수도 2022학년도 86.1점, 2023학년도 88.3점, 2024학년도 89.3점으로 점수가 해마다 올랐다. 2024학년도와 2022학년도 비교 시 3.2점이나 오히려 상승했다.수시 학교 내신 합격 점수는 학생부 교과전형 기준으로 인문계는 2022학년도 2.45등급, 2023학년도 2.34등급, 2024학년도 2.57등급으로 합격선이 다소 불규칙하고, 2024학년도는 2022학년도 합격 점수에 비
-
대입 전략
수능 최저 기준에 사탐 반영하는 대학 많아…자연계 국어·수학 등급 낮으면 '사탐런' 고려를
자연계 학생 중 탐구과목에서 과학탐구(이하 과탐) 두 과목을 선택하는 대신 사회탐구(이하 사탐) 한 과목 또는 두 과목 선택을 고민하는 학생들이 올해도 많을 것으로 예상된다.특히 현재 모의고사 등의 상황으로 볼 때 4~6등급대 학생들이 많이 고민하는 것으로 보인다. 2026학년도에 대입 재도전을 하는 재수생들도 과탐보다는 사탐 과목을 전략적으로 선택하는 경우가 늘고 있다.이 경우 과탐 두 과목 모두 선택한 학생들도 본인이 선택한 과목에서 응시생 수가 줄어 불리해지지 않을까 고민이 클 것으로 보인다.2026학년도에 자연계 학과이지만 수시 수능최저학력기준에서 사탐도 반영하는 대학들이 많다. 고려대, 성균관대, 서강대, 한양대, 중앙대, 경희대, 이화여대, 서울시립대 등 서울권 주요 대학들은 사탐 과목도 수시 최저 등급으로 반영한다. 등급 확보만 되면 과탐 과목과 동급으로 간주해 불이익이 없다. 이 외에 건국대, 동국대, 홍익대, 세종대, 한국외대, 단국대, 아주대, 숙명여대에서도 사탐 과목으로 모두 수시에서 최저 등급으로 인정하고 있다.서울대는 지역균형전형 간호대, 의류학과, 식품영양학과에서 사탐 과목도 수시 최저 등급으로 인정하고 있다. 연세대는 국제형(국내고) 전형 융합과학공학부, 숭실대는 논술 우수자전형에서 인정한다. 인하대는 의예과를 제외하고는 수시에서 최저 반영 과목으로 지정했다. 국민대의 경우 자연계 학과에서는 과탐을 지정해놓은 상황이다.현재 과탐에서 4~6등급대 학생 중 수시에서 수능 최저등급 확보가 매우 중요한 학교 내신 상위권 학생들에게는 전략적 판단을 할 수 있는 상황이다.정시에서는 자연계학과에서 사탐 과목을 인정하지만, 상당수
-
대입 전략
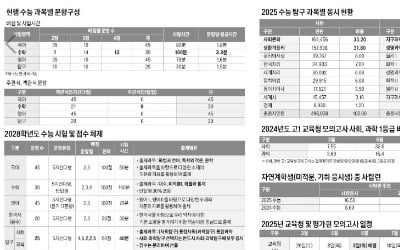
통합과학 영향력 커지고 심화 수학 출제 제외…사탐·과탐 문항 늘고 배점은 3단계로 세분화
올해 고1이 되는 학생부터 적용되는 2028학년도 대입 수능에서는 탐구과목 영향력이 상당히 높아질 것으로 보인다. 현재 탐구과목은 사탐 9과목, 과탐 8과목 중 두 과목을 선택하는 방식이고, 수험생 입장에서 가장 부담이 덜한 과목에 집중적으로 응시하고 있다. 사탐 9과목 중에서는 2025학년도 수능 기준으로 사회문화 33.2%, 생활과 윤리 31.8%로 이 두 과목에 65.0%가 집중됐다. 과탐에서는 8과목 중 지구과학1 36.0%, 생명과학1 32.7%로 두 과목에 집중된 상황이다.2028학년도부터 수험생은 통합사회·통합과학 두 과목에 모두 응시해야 한다. 시험시간 또한 현재 한 과목당 30분이지만, 2028학년도부터는 40분으로 늘어나고 문항 수도 기존 과목당 20문항에서 25문항으로 늘어난다. 수험생 입장에서는 문항 수와 시간이 늘어난 것 자체가 부담일 수 있다.사회·과학에서 두 과목만 선택하는 현재 수능 구도에서 탐구 시험 영역 자체가 17개 영역으로 늘어나고, 문항 수도 늘어난다. 시험 영역 간 통합으로 출제되기 때문이다. 또한 탐구영역의 문항별 배점이 현재 2점, 3점 이원화에서 1.5점, 2점, 2.5점으로 삼원화 체제로 바뀐다. 배점 문항이 세분되어 변별력이 더 높아질 수 있다. 탐구영역은 전반적으로 시험 영역도 확대되었고, 여기에 따라 문항 수, 시험시간, 배점 체제가 모두 늘어나 현재보다 변별력은 더 커질 것으로 보인다.수능 과목 탐구영역은 통합사회·통합과학에서 50문항으로 국어, 수학, 영어보다 많다. 현재까지는 국어 45문항, 영어 45문항, 수학 30문항, 탐구 두 과목 40문항(각 20문항)으로 국어, 영어 문항 수가 가장 많지만 2028학년도부터는 탐구 문항 수가 가장 많게 된다.배점도 현재 국어·
-
대입 전략
수도권 지원 6222명 급증, 지방 3593명 줄어…2026학년도 재수생, 중·하위권대 크게 늘듯
2025학년도 대학입시 지원은 최상위권 의대 집중에 따른 연쇄적 상향 지원 추세가 뚜렷했다.의대 모집 정원 확대로 우선 의대 정시 지원자 수가 지난해 대비 29.9% 증가했다. 치대도 16.4%, 한의대도 10.9%, 약대도 8.3% 지원자가 늘었다. 최상위권이 의대로 빠져나가면서 치대, 한의대, 약대도 합격의 기대심리가 동반 상승했다. 결과적으로 의약학계열 전 부문에 상위권 학생이 몰렸다고 볼 수 있다.그러나 서울대·연세대·고려대(이하 서연고)에서 의대, 치대, 약대, 수의대, 간호대 등 메디컬 관련학과를 제외한 자연계 정시지원은 서울대가 지난해 대비 18.7% 줄어들었다. 연세대도 9.3% 줄었다. 고려대는 29명(0.9%) 늘어나는 것으로 그쳤다. 서연고 전체에서 의약학계열을 제외한 정시 지원자 수는 전년 대비 821명 줄어들었다. 의약학계열과 수능 합격 점수가 비슷한 서울대·연세대 자연계 지원자 수는 지난해보다 서울대 585명, 연세대 265명이 줄었다.서연고 이공계와 의약학계열 동시 합격 가능권 대학에 수능 고득점 학생 상당수가 정시지원 선택을 의약학계열로 했다고 볼 수밖에 없다. 최상위권 수능 고득점 학생들이 의약학계열 지원 규모가 늘어 서연고 자연계열 정시 합격선에 어떠한 변화가 있었는지도 관심이 커지고 있다. 이들 대학의 합격선은 금년도 6월 이후에 공개된다. 2026학년도 수험생에게는 의대 모집 정원의 불확실한 변수가 남아 있는 상황에서 이들 대학의 합격선 변동이 어떻게 나타났는지 주의를 기울여야 한다. 2026학년도 의대 모집 정원이 현재까지도 미확정된 상태이고, 2025학년도 의대 모집 정원이 늘어난 상황에서 합격 점수도 변동이 생겨 2026학년도를 준비하는 수험생에게
-
대입 전략
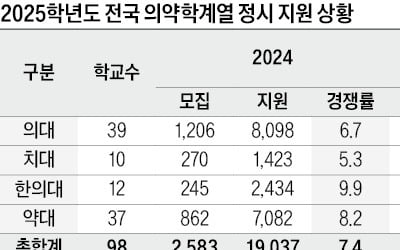
의·치·한·약, 지원 1만9037건…작년보다 18% 급증, 중복합격 다수 예상…추가합격 규모 커질 듯
2025학년도 정시 의대, 치대, 한의대, 약대 메디컬 부문 지원은 2만2546건으로 지난해 1만9037건보다 3509건(18.4%)이 늘어났다. 의대 39개 대학 정시 지원 건수는 1만519건으로 지난해 8098건 대비 2421건(29.9%) 증가했다. 의대, 치대, 한의대, 약대 중 가장 많이 늘어난 수치다. 치대 10개 대학은 1657건, 지난해 1423건 대비 234건(16.4%), 한의대 12개 대학은 2700건, 지난해 2434건 대비 266건(10.9%), 약대 37개 대학은 7670건으로 지난해 7082건 대비 588건(8.3%) 늘어났다.권역별로 서울권이 4629건, 경인권 1673건, 지방권 1만6244건으로 전체 지원 건수는 2만2546건이다. 서울권은 전년 4180건 대비 449건(10.7%), 경인권은 전년 1356건 대비 317건(23.4%) 증가했고, 지방권은 전년 1만3501건 대비 2743건(20.3%)이 늘었다.정시 경쟁률은 의대가 6.6 대 1로 전년 6.7 대 1보다 다소 하락했다. 모집 정원이 전년 1206명에서 1599명으로 32.6%가 늘어난 영향이다. 반면 치대는 전년 5.3 대 1에서 6.1 대 1, 한의대는 전년 9.9 대 1에서 10.5 대 1, 약대는 8.2 대 1에서 9.0 대 1로 경쟁률이 모두 상승했다. 치대, 한의대, 약대는 정원 변동이 크지 않았다.2025학년도 정시 경쟁률에서 의대는 순천향대 의대가 26.19 대 1로 가장 높았고, 다음으로 고신대 25.77 대 1, 동국대(WISE) 16.33 대 1, 단국대(천안) 15.95 대 1, 대구가톨릭대 14.60 대 1 순이었다. 약대는 제주대 약대가 57.00 대 1로 가장 높았고, 계명대 50.00 대 1, 순천대 29.61 대 1, 경북대 13.50 대 1 순이었다.치대는 강릉원주대가 15.33 대 1로 가장 높았고, 다음으로 전북대 9.93 대 1, 전남대 6.92 대 1, 연세대 6.75 대 1, 조선대 6.58 대 1 순이었다. 한의대는 동국대(WISE)가 25.13 대 1로 가장 높았고, 상지대 19.11 대 1, 동신대 16.09 대 1, 대전대 11.31 대 1, 부산
-
대입 전략
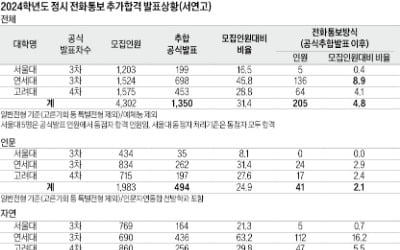
연세대 추가합격자 중 16%가 전화통보로 확정, 내달 19일까지 연락…통화 3번 안 되면 불합격
2024학년도 정시 최초 합격자 발표 이후 서울대·연세대는 각각 3차, 고려대는 4차까지 학교 홈페이지에 추가 합격 인원을 공지했다. 일반전형 기준으로 서울대 3차까지 공식 추가 합격 인원은 199명으로 전체 모집 인원 대비 16.5%다. 연세대는 698명으로 모집 인원 대비 45.8%, 고려대는 453명으로 모집 인원 대비 28.8%다. 서울대·연세대·고려대 전체 1350명이 당시 공식 발표로 추가 합격했다. 공식 발표 이후에는 최종 등록 기간까지 각 대학에서는 전화 등을 활용해 개별적으로 학생들에게 합격 통보를 하고 있다. 이후 7월경에 발표하는 대학 공식 발표에서는 최종 추가 합격 순위를 알 수 있어 전화 통보 방식 등을 활용한 정시 추가 합격 인원을 추정할 수 있다. 2024학년도 최종 추가 합격 인원은 1350명에서 205명이 늘어난 1555명이다. 전체 모집 인원 대비 4.8%가 전화 통보 방식 등으로 공식 발표 이후 추가로 합격한 인원이다.서울대는 3차까지 추가 합격 인원이 199명이고, 최종 추가 합격 인원은 204명으로 공식 발표 이후 5명이 추가됐다. 서울대 5명은 동점자였고, 서울대 동점자 처리 기준에 따라 모두 동시 합격 처리됐다. 서울대 인문계의 경우 3차 공식 발표와 최종 추가 합격 인원이 35명으로 동일했다. 자연계의 경우 공식 발표는 164명이었나 동점자 5명이 추가로 합격해 최종 169명으로 늘어났다. 동점 합격자가 발생한 학과는 지구과학교육과 1명, 약학계열 1명, 조경지역시스템공학부 1명, 산림과학부 1명, 생명과학부 1명으로 모두 자연계 학과에서 5명이 나왔다.연세대는 공식 발표 3차까지 추가 합격한 인원이 698명으로 전체 모집 인원의 45.8%였다. 공식 발표 이후 최종 추가 합격 인원은 834명이었
-
대입 전략
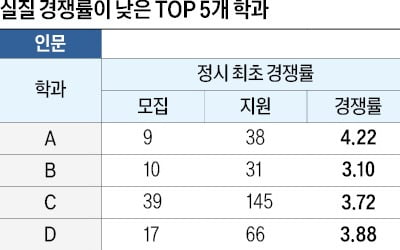
서울 소재 대학, 추가합격 포함 실질 경쟁률 '2.6 대 1', 올해 추가합격 크게 늘듯…종합판단 후 지원해야
2024학년도 서울 소재 28개 대학을 조사한 결과 정시 평균 경쟁률은 5.54 대 1이었다. 최종 정시 추가 합격자까지 고려하면 실질 경쟁률은 2.60 대 1로 크게 낮아졌다. 28개 대학 인문계 모집 인원은 1만862명으로 5만9224명이 지원해 정시 평균 경쟁률은 5.45 대 1이었다. 이후 정시 추가 합격자가 1만1500명이 나와 최종 합격자는 2만2362명으로 늘어났다. 지원자 5만9224명 대비 실질 경쟁률은 2.65 대 1이다.자연계는 자연계 모집 인원이 없는 1개 대학을 제외하고 27개 대학을 조사한 결과, 모집 인원 1만2137명에 지원자 6만8227명으로 정시 평균 경쟁률은 5.62 대 1이었다. 이후 1만4568명이 정시 추가 합격해 최종 합격자가 2만6705명으로 늘었다. 지원자 6만8227명 대비 실질 경쟁률은 2.55 대 1로 크게 하락했다.인문계 28개 대학 중 실질 경쟁률이 2 대 1 미만인 대학도 2곳이 나왔다. 정시 최초 평균 경쟁률은 4.57 대 1이었으나 추가 합격자까지 고려한 실질 경쟁률은 1.96 대 1이었다.추가 합격을 고려한 실질 경쟁률이 2 대 1에서 3 대 1 미만인 대학도 20곳이다. 전체 대학 대비 비중이 71.4%다. 이들 20개 대학의 정시 최초 평균 경쟁률은 6.10 대 1이었으나 추가 합격자까지 고려하면 실질 경쟁률이 2.54 대 1로 크게 하락했다.인문계열에서 경쟁률 3 대 1 이상인 대학은 6개 대에 불과했고, 4 대 1을 넘는 대학은 없었다. 3 대 1 이상인 대학은 서울대·연세대·고려대 등 6개 대학으로 정시 최초 평균 경쟁률은 4.19 대 1이었으나 추가 합격을 고려하면 3.23 대 1로 떨어졌다.자연계열에서는 27개 대학 분석 결과 추가 합격 고려해 경쟁률 2 대 1 미만인 대학이 2개다. 이들 2개 대학 정시 최초 평균 경쟁률은 4.55 대 1이었으나 정시 추가 합격자를
-
대입 전략
서·연·고 최저 합격선 인문 386점, 자연 384점…의대는 수도권 408점, 지방은 402점
2025학년도 수능 결과 국어, 수학은 지난해보다 쉽게 출제되어 표준점수 기준으로 합격선이 지난해보다 내려갈 것으로 보인다. 국어는 지난해 표준점수 최고점 기준으로 11점 하락, 수학은 8점 하락했다.반면 탐구 영역은 대체로 어렵게 출제되어 표준점수 기준으로 합격선 상승이 예상된다. 사탐 9과목 중 경제, 사회문화, 정치와 법을 제외한 6과목이 상승했으며, 이 중 생활과 윤리는 지난해 65점에서 77점으로 12점이나 올랐다. 지난해 9과목 중 1등급 커트라인이 만점 과목만 생활과 윤리, 윤리와 사상, 한국지리, 세계사 등 4개 과목이었으나, 이번 수능에서는 1등급 커트라인이 만점으로 추정되는 과목은 없다.과탐은 지구과학1, 생명과학1 2과목은 지난해 대비 각각 4점과 1점 상승했고, 지구과학2는 지난해와 동일했다. 과탐의 경우 8과목 중 5과목이 하락해 자연계 학과 합격선도 과탐 기준으로 표준점수 기준 합격선이 하락할 것으로 예상된다.2025학년도 정시 합격선은 국수탐 합산 600점 만점(표준점수) 기준 서울대·연대·고대 인문계열 최저선은 386점, 자연계열은 384점, 주요 10개 대학 기준 인문계열은 369점, 자연계열은 372점이 예상되고, 인서울 최저선은 인문계열 333점, 자연계열 342점이 예상된다.주요 대학별로는 인문계열의 경우 최저선으로 서울대 393점, 연세대·고려대 386점, 성균관대·서강대 382점, 한양대 379점, 중앙대 376점, 경희대 369점, 자연계열은 서울대 391점, 연세대·고려대 384점, 성균관대·서강대·한양대 380점, 중앙대 374점, 경희대 372점으로 전망된다.인문계열 학과별로는 서울대 경영대학 401점, 정치외교 400점, 연세대 경영 396점, 고려대 경영대학 396점으로 지