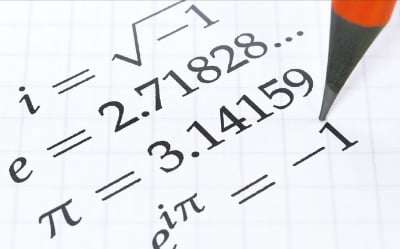생글생글

학습 길잡이 기타

MRI·노이즈캔슬링 기술 뒤엔 복소수 작동하죠

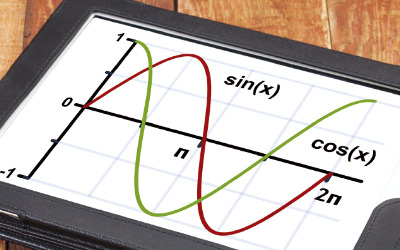
▶ 지난 생글생글 제897호에 이어서 계속코일과 콘덴서가 복소평면의 반대 방향에 위치하게 되는 것은 단지 계산상 편의가 아니라 전류와 전압의 실제 시간차를 수학적으로 정확히 반영한 결과다. 복소평면은 단순한 좌표 공간이 아니다. 그것은 시간의 흐름, 에너지의 진동, 신호의 패턴을 하나의 수로 응축한, 수학의 가장 정교한 지도다.복소수와 복소평면의 도입은 단지 수학적 표현의 변화가 아니라, 전기 기술 전반의 획기적인 도약을 이끌어냈다. 복소 임피던스를 이용한 회로 해석은 전력 손실을 줄이고, 안정적인 송전과 효율적인 설계를 가능하게 했다. 특히 대규모 송전망, 예를 들어 한전의 154kV 변전소와 같은 고전압 시스템에서는 각 부품의 위상 특성을 고려해 전체 회로의 동작을 해석해야 한다. 이때 복소수 기반의 임피던스 계산과 위상 분석은 전압 강하, 전력 손실, 공진 주파수 등을 정확히 예측하고 설계하는 데 핵심이 된다.진동하는 소리나 전기 신호는 시간에 따라 변하는 파형으로 표현된다. 수학적으로는 사인 함수나 코사인 함수, 즉 삼각함수의 조합으로 나타난다. 그런데 이런 복잡한 파형을 더 간단하게 다루기 위해 수학자들은 놀라운 방법을 개발했다. 바로 푸리에 해석(Fourier Analysis)이다. 이 방법은 어떤 복잡한 신호도 단순한 주파수들의 합으로 쪼갤 수 있다는 원리다. 그런데 이 주파수 하나하나는 단지 진동수만 있는 것이 아니라, 위상(언제 시작되는가)과 진폭(얼마나 강하게 울리는가)도 함께 가진다. 예를 들어, 어떤 음파가 440Hz(피아노의 ‘라’음)에 해당하는 사인파로 구성되어 있다면, 그 신호는 시간에 따라  같은 식으로 표현된다. 하지만 이 신호가 단순한

학습 길잡이 기타

전기의 진동, 빛의 파동…허수가 문제 푸는 열쇠죠

허수는 처음엔 받아들이기 어려운 개념이었다. 실수처럼 눈으로 볼 수도, 손으로 측정할 수도 없기 때문이다. 그러나 계산 속에서 그 존재는 점점 더 명확해졌다. 삼차방정식을 풀던 과정에서, 전기회로의 진동을 분석할 때, 빛의 파동과 소리의 진동을 수식으로 설명할 때, 허수는 실수보다 더 자연스럽게 문제를 해결하는 열쇠가 되었다.우리는 허수를 기호 i로 표현하기로 약속했다. 이때 i는 i2=-1이라는 관계를 갖는 특별한 수로, 실수로는 도저히 표현할 수 없는 새로운 수의 세계를 열어준다. 이 허수는 단독으로 존재하기보다 실수와 결합해 함께 나타나는 경우가 많다. 예를 들어 a+bi라는 형태는 하나의 수처럼 보이지만, 사실은 실수 a와 허수 b가 함께 있는 형태로, 이를 ‘복소수’라고 부른다.복소수는 특별한 점이 하나 있다. 바로 시각화가 가능하다는 점이다. 예를 들어, 우리가 중학교 수학 시간에 x+y=3 같은 방정식을 그래프로 그릴 때, x축과 y축을 기준으로 직선이나 곡선을 표현했던 것을 떠올려보자. 복소수도 마찬가지로 표현할 수 있다. 다만 여기서 축은 우리가 익숙한 ‘x, y’가 아니라, 실수 부분은 가로축, 허수 부분은 세로축에 두는 것이다. 가령 3+4i가 있다고 하면 우리가 알고 있는 좌표 (3, 4) 위의 한 점으로 대응시키는 것이다. 이 공간을 우리는 ‘복소평면(complex plan)’이라고 부른다.이 복소평면에서 복소수는 단순한 좌표가 아니라 벡터로 생각할 수 있다. 즉 방향과 길이를 가진 화살표처럼 이해할 수 있는 것이 또 다른 장점이다. 예를 들어 3+4i는 길이 가 되고, 방향은 실수축과 이루는 각도로 표현할 수 있다.이 구조의 진가는 곱셈이나 나눗셈을 할 때 드러난다.

학습 길잡이 기타

'상상의 수'로 자연현상 파악의 한계를 보완