생글생글

학습 길잡이 기타

2차 관계식은 도형의 완벽함 그려내는 마법 주문

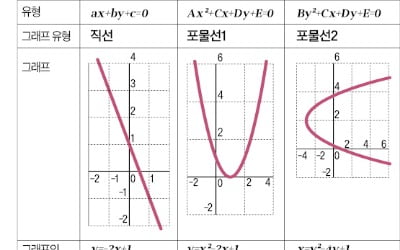
Ax2 + By2 + Cx + Dy + E= 0라는 복잡한 식을 보면 머리가 지끈지끈 아파올 수도 있습니다. 하지만 이 식 속에 눈에 보이지 않는 아름다운 도형의 세계가 숨어 있다면 믿으시겠습니까? 일차식인 이 좌표평면 위에 단순하고 명확한 직선을 그려내듯, 이 딱딱한 이차 관계식 또한 단순한 계산식이 아닙니다. 이 식은 곧 좌표평면 위에 도형의 완벽함과 우아함을 그려내는 마법의 주문입니다. 이제 그 신비로운 변신 과정을 함께 확인해보시죠.자, 이제 미지수가 x, y 2개인 이차방정식의 일반형을 떠올려봅시다.Ax2 + By2 + Cx + Dy + E= 0이 복잡한 식을 그래프로 나타낼 수 있을까요? 물론입니다. 오늘은 이차 관계식에 대해 생각해보려고 합니다. 우리가 이차 관계식을 이야기할 때, 적어도 x2이나 y2항은 하나라도 있어야 의미가 있습니다. 먼저 A는 0이 아니고 B가 0인 경우를 생각해보겠습니다. 이때 방정식은 Ax2 + By2 + Cx + Dy + E= 0의 형태가 됩니다. 이 식을 y에 대해 정리하면 다음과 같이 됩니다(단, D=0이라고 가정합니다).Dy=−Ax2−Cx−E 양변을 D로 나누어 정리하면,이는 결국 우리가 익히 아는 y=ax2 + bx +c 꼴의 이차함수로 귀결됩니다. 이 함수를 좌표평면 위에 그리면 바로 포물선이 됩니다. 중학교 3학년 과정에서 배우는 것처럼, 이차항의 계수의 부호에 따라 그래프의 모양이 결정됩니다. 계수가 양수면 아래로 볼록한 포물선이, 음수면 위로 볼록한 포물선이 그려지게 됩니다. 이처럼 복잡해 보이던 이차 관계식의 특정 조건이 곧 우리에게 익숙한 포물선을 그려내는 셈입니다. 그렇다면 이번에는 A=0이고 B가 0이 아닌 경우를 생각해봅시다. 이때 방정식은 By2+Cx+Dy+E=0의 형태가 됩니다.이 식을 x에 대해 정리하면, ‘

학습 길잡이 기타

포물선·타원·쌍곡선 모두 x와 y 이차식 표현 가능

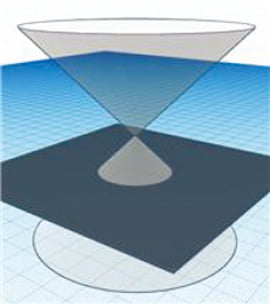
안녕하세요! 오늘은 수학에서 매력적인 주제 중 하나인 이차곡선에 관해 이야기해보려 합니다. ‘이차곡선’이란 이름이 아직은 낯설게 들릴 수 있지만, 사실 중학교와 고등학교에서 접하는 곡선들이 바로 이차곡선에 해당합니다. 예를 들어, 중학교 3학년 때 배우는 포물선(이차함수)부터 시작해 고등학교 1학년 과정에서 등장하는 원, 그리고 선택과목인 기하에서 만나게 될 포물선, 타원, 쌍곡선이 모두 이차곡선입니다.수학자들이 이들을 한 그룹으로 묶어 ‘이차곡선’이라고 부르는 이유는 이 곡선들을 모두 x와 y의 이차식으로 표현할 수 있기 때문입니다. 이렇게 모양이 다양한 곡선이 서로 연결된 점이 있다는 사실이 꽤 흥미롭죠.오늘은 이차곡선의 정의와 각각의 특징을 살펴보면서 함수식을 몰라도 이차곡선이 왜 독특한 주제인지 알아보려고 합니다. 또한 기하학적으로 이 곡선들이 어떻게 나타나는지 함께 살펴볼 텐데, 이를 통해 수학적 개념을 보다 넓은 시각에서 바라보고, 수학이 서로 어떻게 연결되어 있는지 확인할 수 있을 것입니다.이 곡선들을 하나로 묶어 바라보기 시작한 건 상당히 오래되었습니다. 그리스 수학자 아폴로니우스가 그 주인공으로 알려져 있는데, 이 곡선들을 하나의 원뿔에서 모두 발견할 수 있기 때문에 이러한 이차곡선을 ‘원뿔곡선’이라고 부르기도 합니다.조금 인위적이기는 하지만, 두 원뿔이 서로 꼭짓점을 맞대고 대칭으로 놓인 원뿔이 있다고 상상해봅시다. 그러니까 y=x 그래프를 y축을 축으로 회전시킨 회전체라고 생각하면 편하겠네요. 이제 상상 속 이 회전체를 밑면과 평행하게 자른다면 그 단면은 무엇이 될까요? 상상을 잘 따라오고