생글생글

과학과 놀자

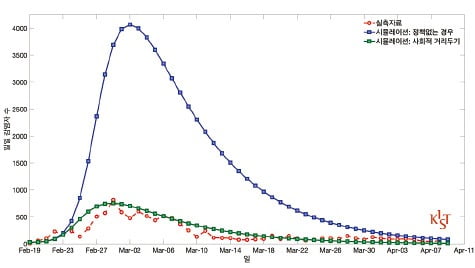
'나비효과' 활용한 코로나19 확산 시뮬레이션 모델…사회적 거리두기 등 방역정책의 효과 과학적으로 증명

신종 코로나바이러스 감염증(코로나19)이 세계를 강타했다. 감염자 수는 한 해가 지난 지금도 줄어들지 않고 여전하다. 감염성 질병은 어떻게 전파되는가? 질병이 감염되고 확산되어 가는 것은 사람들 사이에 소문이 전파되는 것이나 뉴런 사이에서 정보가 퍼져나가는 것과 본질적으로 같은 현상이다. 이들 현상을 하나의 모형으로 만드는 데는 2020년 현재 (1)미분방정식 방법을 사용하거나 (2)복잡계에 기반해서 대용량 슈퍼컴퓨터를 이용하는 방법이 있다. 둘 다 응용수학의 한 갈래인데, 시뮬레이션(시늉내기, 전산모사)을 진행할 때 어디에 초점을 두는가 하는 점이 다르다.  미분방정식을 활용한 질병전파 모델미분방정식 방법을 이용하는 경우는 사회 구성원을 하나의 큰 떼(무리, 덩어리)로 본다. 주로 ‘S-(E)-I-R 모형’을 활용하는데, SEIR는 (정상인)감염 대상군(Suspectible), 질병 노출(Exposed), 감염(Infectious), 회복(Removed)의 영어 단어 앞 글자를 따온 말이다. 미분방정식을 쓴다는 것은 욕조에 물을 채우는 상황에 비유될 수 있다. 감염인구 무리를 하나의 욕조라고 한다면, 여기에 물을 채우는 수도꼭지는 감염률이 된다. 이들 수도꼭지를 열고 닫는 것은 질병의 특징으로서 전염 강도 및 감염인구와 비감염인구의 접촉 수에 의해 결정된다. 그리고 물을 빼는 배수꼭지는 회복률로 비유된다. 이 S-I-R 모형은 1927년 영국 생화학자 W O 커맥과 병리학자 A G 매켄드릭이 질병 유행의 초기 조건과 확산 정도를 예측하기 위해 사용하면서 처음 제안됐다.S-E-I-R 모형은 S와 I 사이에 접촉군 단계 (E)를 추가한 모형이다. 즉 잠복기가 고려되어 있다. 인구 떼(무리)의 상태를 늘림으로써 다양한 모형을 만들거나

진학 길잡이 기타

함수의 연속성과 미분가능성

함수의 연속성을 나타내는 수식적 표현을 바탕으로 이를 도함수의 정의에 적용하는 형태의 논제가 꾸준히 출제되고 있다. 이런 논제 해결을 위해서 함수의 연속성을 나타내는 다양한 형태의 수식적 표현 방법을 숙지하고, 이를 논제에 올바르게 적용하는 반복적인 연습이 요구된다. ☞ 포인트수리논술의 본질은 ‘출제자와의 소통’이다. 출제자가 묻고 있는 것을 정확히 파악하는 것이 소통의 기본이며, 문제 해결을 위해 출제자가 던져준 여러 도구 즉, 제시문과 조건 등을 적절한 시기에 올바르게 사용하는 것이 이런 소통을 더 매끄럽게 할 수 있도록 도와준다. 직접적인 도구가 보이지 않는 경우에는 문항 배치의 순서에서 출제자가 의도한 맥락적 흐름을 파악할 수도 있다.