생글생글

대입전략

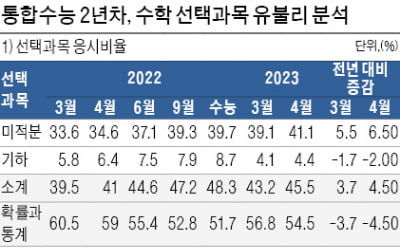
6월 모평 후 이과 반수생 몰리면 격차 더 벌어질 듯…올 3월 수학 1등급 내 이과생 비중 92.8%까지 상승

통합수능 2년차, 수능 수학에서 이과생 강세 현상은 더 뚜렷해질 것으로 예상된다. 올해 수학에서 문이과 유불리 문제를 짚어보고 입시전략을 분석한다.전년 대입에서 최대 이슈는 수학에서 선택과목에 따른 문이과 유불리 문제였다. 전년 수능에서 수학 1등급 내 이과생(미적분 또는 기하 응시) 비중은 84.9%에 이르는 것으로 추정된다. 사실상 상위 등급을 이과생이 휩쓸었다. 표준점수도 이과생이 앞섰다. 미적분과 기하의 표준점수 최고점은 147점으로 확률과통계의 144점을 3점이나 앞섰다. 전년 통합수능 첫해, 이과생의 ‘문과침공’ 현실화이과생들은 수학에서의 강세에 힘입어 인문계 학과로 대거 교차지원에 나섰다. ‘문과침공’이란 표현이 등장했을 정도다. 한 예로, 지난해 서울대 정시모집 최초합격자 결과는 충격적이었다. 서울대 인문·사회계열 학과 최초합격자 중 44.4%가 이과생으로 확인됐다. 자유전공학부 합격자 중 94.6%, 심리학과 합격자 중 88.9%가 이과생이었다.지난해 모의고사 내내 수학에서 이과생은 문과생을 압도했다. 지난해 1등급 내 이과생 비중 추정치는 모의고사별로 최저 79.7%에서 최고 95.1%의 분포를 보였다. 문이과 격차는 올해 더 벌어졌다. 지난 3월 학력평가에서 수학 1등급 내 이과생 비중은 92.8%로 추정된다. 지난해 3월 89.5%보다 3.3%포인트나 높아졌다. 올해 3월 2등급 내 이과생 비중도 76.8%에 달한다.표준점수 최고점 격차도 여전하다. 3월 학력평가에선 미적분 164점, 확률과통계 158점으로 7점 차까지 벌어졌다. 4월 학력평가의 경우 미적분 160점, 확률과통계 154점으로 6점 차로 추정된다.이 같은 추세는 올해 심화할 것으로 예측된다. 문이과 격차는 구조

커버스토리

문·이과 통합수학 시대…'마인드 리셋' 필요해요

‘문과·이과 통합 수학’ 시대입니다. 지난해 11월 치러진 수능 시험에서 처음 적용됐어요. 반응과 평가가 엇갈립니다. 문과생들이 손해를 봤다, 별 차이가 없다는 말이 각각 존재합니다. 수학이 어떤 얼굴을 하고 있든, 우리는 수학을 피해서 갈 수 없습니다. 국·영·수 아닙니까. 생글이 여러분을 잠시 최면 상태로 초대하겠습니다. “여러분은 언제부터 수학이 싫어지기 시작했는지 기억하십니까? 반대로 수학이 언제부터 좋아졌는지 기억나세요? 지금부터 여러분은 수학을 대하는 마인드를 바꾸게 될 것입니다. 레드 썬!” 생글은 이번 호에 ‘수포자’였던 남호성 고려대 영어영문학과 교수님의 사례를 소개합니다. 교수님은 학생 여러분이 수학 마인드를 리셋(reset)할 것을 간절하게 원합니다. 수학문제를 이렇게 풀어라, 저렇게 풀어라라고 말하지 않습니다. 수학을 멀리하게 만드는 나쁜 생각을 버릴 것을 권합니다. 그의 당부는 아마도 다른 과목에도 적용할 수 있을 것입니다. 남 교수님이 최근 출간한 책 《수학을 읽어드립니다》는 여러분의 수학관을 크게 변화시킬 것입니다.고기완 한경 경제교육연구소 연구위원

커버스토리

'수포자'였던 영문과 교수가 AI 연구…수학에 눈뜨니 다른 세상이 보이네요

인공지능(AI)은 수학의 집합체다. AI에 필수적인 데이터 처리, 머신러닝 등은 함수, 미분, 확률 등 수학을 바탕으로 한다. 그런 AI를 문과생이 개발한다면 곧이곧대로 믿어지지 않는다. 남호성 고려대 영어영문학과 교수가 설립해 이끌고 있는 남즈연구소는 AI에 필요한 음성 인식, 음성 합성 등의 원천 기술을 보유하고 있다. 그런데 연구원 30여 명 중 이공계 출신은 한 손에 꼽을 정도다. 남 교수부터 문과 출신이고, 대부분 영문과 국문과 등 인문계 대학원생과 대학생이다.남 교수는 영문과 교수가 수학과 코딩을 가르치고 AI 기술까지 개발한 사연을 담아 지난달 《수학을 읽어드립니다》(한국경제신문)를 출간했다. 서울 동소문동 남즈연구소에서 그를 만났다. 남 교수는 “나도 고등학생 땐 수포자(수학을 포기한 사람)였다”고 했다. 보통의 문과생들처럼 수학이 싫어 문과를 택했다. 그가 수학과 다시 마주한 것은 대학에서 음성학이라는 분야를 접하면서다. 음성학에서는 말을 글자 단위, 발음 단위로 쪼개 연구한다. 그 과정에서 수학적 기법을 활용한다.다시 만난 수학은 고교 때 알던 수학과는 달랐다. 공식을 달달 외울 필요가 없고 복잡한 계산도 하지 않아도 됐다. 남 교수는 “사람 말소리의 높낮이를 그림으로 표현하면 사인, 코사인 곡선이 나온다”며 “고등학교 때 무슨 의미인지도 모르고 배웠던 수학을 완전히 다른 방식으로 이해하게 됐다”고 말했다. 그는 깨달았다. 수학은 그저 세상일을 수식으로 표현한 것에 불과하구나.깨달은 것은 또 있었다. 그는 “문과를 택하면서 수학에서 해방됐다고 생각했지만 사실은 수학을 공부할 권리를 박탈당했던 것”이라고 말했

커버스토리

벡터·함수·미분·확률…수학과 화해해요

수학을 싫어하게 된 결정적 시기가 여러분에게 있었을 것입니다. 초등 고학년? 중학교? 고등학교? 셋 중 하나죠. 수학을 좋아하게 된 계기도 있었을 것입니다. 100점을 맞았다든가, 좋아한 쌤이 수학쌤이었다든가, 그런 거죠. 전부가 수학을 잘할 필요는 없지만, 수학에 적대적일 필요는 없지요. 수학은 언제나, 누구에게나 애증의 과목이니까요. #1. 결정적 계기 만나기수학자 중에 앤드루 와일즈라는 사람이 있어요. 인류 최대의 난제라는 ‘페르마의 마지막 정리’를 300여 년 만에 증명한 수학자죠. 17세기 프랑스 수학자 피에르 드 페르마가 낸 문제는 단순했습니다. [Xn+Yn=Zn. n이 3 이상의 정수일 때 이 방정식을 만족하는 정수해 x, y, z는 존재하지 않는다]였죠. 그가 수학을 좋아하게 된 결정적 계기는 1963년 찾아 왔습니다. 학교 수업을 마치고 우연히 마을 도서관에 들어간 열 살짜리 아이는 《최후의 문제》라는 책 속에서 이 문제를 만났습니다. 아이는 문제 모양이 신기하다고 생각했습니다. 이 아이가 평생 ‘페르마의 마지막 정리’에 꽂혀서 끙끙거리게 될지 누가 알았겠습니까. 앤드루 와일즈는 1993년 6월 영국 케임브리지대학에서 수많은 사람이 보는 가운데 풀었습니다. 마을 도서관, 《최후의 문제》라는 책…, 수학이 좋아지게 되는 계기를 만나면 좋겠습니다. #2. 수학과 화해하기수학을 대하는 마인드와 시각을 바꾸는 첫째 화두는 ‘수학과 화해하기’입니다. 이과생들은 수식이 가득한 책을 줄줄 읽고, 문제를 보면 바로 풀 것이라고 문과생들은 오해하죠. 아닙니다. 이과생도 수학을 싫어하고 잘 못합니다. “수학이 내 적성과 맞지 않구나”라며 지레 겁을 먹