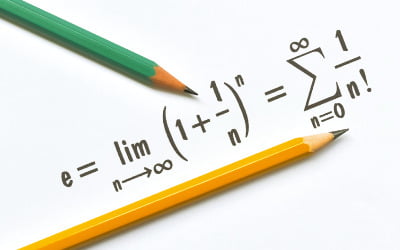생글생글

재미있는 수학

"존재하지도 않는 허수, 대체 왜 배우죠?"…화가 난 수포자를 달래봅시다 [재미있는 수학]

얼마 전 고교 1학년 공통수학1에서 복소수 단원을 수업할 때였습니다. 제곱해서 -1이 되는 수, 눈에 보이지 않고 실생활에서 손에 잡히는 수도 아닌 ‘상상의 수(Imaginary Number)’를 마주한 학생들의 표정은 당혹감 그 자체였습니다. “선생님, 존재하지도 않는 수를 대체 왜 배워야 하나요?” 이런 질문을 받을 때마다 저는 소설 <박사가 사랑한 수식>을 떠올립니다. 이 작품은 수가 단지 계산을 위한 기호가 아니라, 사람과 사람을 잇고 세상을 새롭게 바라보게 하는 언어일 수 있기 때문입니다.2004년 요미우리 소설상과 제1회 서점대상을 수상한 이 소설의 주인공 ‘박사’는 한때 촉망받던 수학자였습니다. 하지만 불의의 사고로 기억이 딱 80분간만 지속되는 병을 앓고 있습니다. 80분이 지나면 그의 기억은 깨끗하게 지워집니다. 그런 박사가 세상과 소통하기 위해 선택한 유일한 언어가 바로 ‘수학’입니다.박사의 집에 새로 온 ‘가정부(나)’와 그녀의 열 살짜리 아들은 숫자를 통해 박사의 마음속으로 들어갑니다. 매일 아침 기억을 잃은 박사에게 자신을 다시 소개해야 하는 상황에서도 그들은 숫자가 가진 따뜻한 온기에 기대어 80분이라는 한계를 넘어선 깊은 유대감을 쌓아갑니다.박사는 누군가와 대화를 시작할 때 신발 사이즈나 전화번호를 묻곤 합니다. 그것은 단순한 호구조사가 아니라, 상대방의 존재를 수학적 의미로 받아들이려는 그만의 다정한 인사법입니다. 어느 날 박사는 가정부의 생일인 2월 20일을 세 자릿수로 표시한 220과 자신이 대학 시절 논문상으로 받은 손목시계의 번호가 ‘284’라는 것을 발견하고 깊이 감동합니다. ‘우애수(Amicable Numbe

학습 길잡이 기타

왜 맞는지 설명 못하면, 안다고 할 수 있나?

“소수(prime number)는 끝이 있을까요?” 질문은 단순합니다. 초등학생도 이해할 수 있지요. 하지만 누군가가 “아니요, 소수는 무한히 많아요”라고 대답했을 때, 우리는 곧 되묻게 됩니다. “왜요?” 이 짧은 질문이 바로 수학의 출발점입니다.수학은 ‘맞다’고 믿는 사실조차도 논리로 다시 묻습니다. 단순한 계산을 넘어 그 사실이 왜 그런지, 항상 그런지, 다른 경우엔 안 그런지를 철저히 밝히는 학문입니다. 그래서 수학은 증명을 사랑합니다.소수가 무한하다는 명제를 고대 그리스의 수학자 유클리드는 단 다섯 줄로 증명했습니다. 이미 알려진 소수들을 전부 곱하고, 거기에 1을 더해보지요. 예를 들어, 2×3×5=30, 여기에 1을 더하면 31입니다. 이 수는 앞의 소수들(2, 3, 5)로 나누어지지 않습니다. 그렇다면 31은 그 자체로 새로운 소수이거나, 적어도 지금까지의 소수 목록에는 없는 소수로 나누어져야 합니다.즉 아무리 많은 소수를 알고 있다고 해도 그 바깥의 소수를 찾아낼 방법이 항상 존재합니다. 이 짧은 증명은 명쾌하게, 그리고 단단하게 진실을 밝혀냅니다. 보지 않아도, 세지 않아도, 실험하지 않아도 알 수 있는 진리. 이것이 수학에서의 ‘증명’입니다.우리가 일상에서 “보면 알잖아요”, “느낌이 그렇잖아요”라고 말하는 많은 것이 수학에서는 받아들여지지 않습니다. 수학은 ‘당연한 것’조차 증명을 요구합니다.실제로 수학자 화이트헤드와 러셀은 ‘1+1=2’라는 명제를 증명하는 데 379쪽에 이르는 논리를 펼쳐야 했습니다. 그것은 지나친 집착이 아니라, 생각의 기반을 가장 아래에서부터 다시 점검하려는 시도였습니다. 수

학습 길잡이 기타

소수 기반 RSA 해독…사막서 바늘찾기 만큼 어렵죠

“암호 편지 한 장이 한 나라의 여왕을 단두대로 이끌었다면, 우리는 암호를 단지 숫자의 장난으로 볼 수 있을까?”1586년, 스코틀랜드의 여왕 메리 스튜어트는 옥중에서 편지를 보냈다. 그 편지는 치밀하게 암호화된 기호와 문자로 이루어진 정치적 음모의 기록이었다. 여왕은 잉글랜드의 엘리자베스 1세를 암살하려는 계획을 동료들과 공유했고, 그 내용을 철저히 숨겼다. 그러나 영국의 정보국이 암호문을 가로챘고, 토머스 펠리페스라는 수학자이자 암호 해독가는 그 안의 규칙을 해석해냈다. 그날 단두대에 오른 것은 여왕 한 사람의 운명만이 아니었다. 암호가 역사의 흐름과 권력의 균형을 바꾼 순간이었다.메리 스튜어트가 사용한 암호는 단순한 단일 치환 암호였다. 알파벳을 일정한 기호나 다른 문자로 바꾸는 방식으로, 당시로서는 강력한 보안 기술이었다. 예를 들어 A는 △, B는 □, C는 ☆ 등으로 바뀌고, 특정 단어들은 전체 기호 하나로 요약되기도 했다. ‘Queen(여왕)’은 하나의 상징 기호로, ‘Death(죽음)’는 약어처럼 표현했다.하지만 이 암호는 결국 문자의 등장 빈도와 반복 주기를 분석하는 수학적 방식에 의해 해독되었다. 펠리페스는 편지 전체에서 반복되는 기호를 세어, 가장 많이 등장하는 기호가 영어의 ‘E’일 가능성이 높다는 점에 착안했다. 그리고 그 주기를 파악해 특정 간격마다 나타나는 기호의 구조를 분석했고, 그 주기 길이가 소수(예: 7)일 때 해독이 가능하다는 사실을 알아냈다. 소수 간격에서 나타나는 반복은 암호문의 패턴을 읽어내는 결정적 열쇠가 되었다.이런 방식은 훗날 더 정교한 암호 체계로 발전했다. 특히 오늘날 가장 널리 쓰이는 공개

학습 길잡이 기타

주파수 '소수'로 배치하면 안정적 데이터 전송

1과 자기 자신으로만 나누어지는 수, 소수(素數). 이 단순한 정의 속에는 수학의 신비와 미해결된 수많은 문제가 숨어 있다.초등학교에서 배운 소수(小數, decimal)는 분수를 십진법으로 표현하는 것이었지만, 중학교에 올라가 마주한 소수(素數, prime number)는 전혀 다른 세계의 개념처럼 느껴졌다. 숫자 대신 문자가 등장하고, 3.14 대신 ‘파이(π)’를 사용하며, 익숙했던 소수와 완전히 다른 ‘나누어지지 않는 수’를 배우는 순간, 나는 이 새로운 개념에 신선한 충격을 받았다.그렇다면 소수란 무엇일까? 1과 자기 자신으로만 나누어지는 수, 그것이 바로 소수다. 하지만 이 단순한 규칙을 따르는 숫자들이 왜 그토록 중요한 의미를 가질까? “이 소수는 대체 어디에 쓰이는 걸까?” 세상의 모든 것이 실용적인 의미를 가져야 한다고 믿는 나에게, 그리고 나와 같은 궁금증을 가진 사람들에게 이 질문에 대한 답을 찾아보고자 한다.지난 칼럼에서 건축물에서 공진 현상을 방지하기 위해 소수 간격을 활용하는 방법을 소개한 바 있다. 흥미롭게도, 이 개념은 무선통신에도 동일하게 적용된다. 무선 주파수가 겹치면 서로 다른 신호 간 간섭이 발생해 통신 품질이 저하된다. 이를 방지하기 위해 소수를 기반으로 채널을 할당하는 방법이 사용된다. 소수 간격으로 주파수를 배치하면 특정 신호들이 배수 관계를 이루지 않게 되어, 서로 간섭 없이 안정적인 데이터 전송이 가능하다. 이는 우리가 일상적으로 사용하는 와이파이, 휴대전화 통신, GPS 신호 등에서 필수적인 원리로 작용한다.소수는 지구상의 통신을 안정화하는 것에서 그치지 않는다. 우주 신호를 분석하는 데에도 소수가 활용된다. 최근