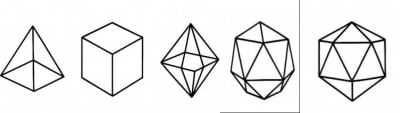
#수학적 아름다움
-
학습 길잡이 기타
'원뿔곡선=2차곡선'…수학언어로 짜여진 우주 비밀
고대의 수학자들이 순수한 호기심으로 발견한 이 네 가지 ‘원뿔 곡선(Conic Sections)’이 먼 훗날 A와 B라는 계수의 조건만으로 완벽하게 분류되는 ‘2차 곡선(Quadratic Curves)’과 정확히 일치한다는 사실은, 이 우주가 얼마나 수학적인 언어로 아름답게 짜여 있는지를 보여주는 매우 강력한 증거 중 하나입니다. 우리는 딱딱한 대수학의 방정식을 풀었을 뿐인데, 그 끝에서 원뿔을 자르던 고대 수학자의 빛나는 호기심과 마주하게 된 것입니다.
-
학습 길잡이 기타
구조적 완전함, 수학적 아름다움의 결정체
아름답다는 것은 무엇일까? 그 기준은 시대에 따라 끊임없이 변해왔다. 중세와 르네상스 시대에 이르러 아름다움은 비례, 균형, 그리고 대칭 속에서 찾을 수 있는 질서로 여겨졌다. 사람들이 가장 아름답다고 여긴 조각상은 고대 그리스의 비너스상과 르네상스 시대 미켈란젤로의 다비드상이었다. 이 조각들은 모두 인체의 황금 비율, 균형 잡힌 근육 구조, 자연스러운 역동성을 지니고 있다. 회화에서도 아름다움은 인체뿐 아니라 풍경과 구도 속에 담겼다. 레오나르도 다빈치의 모나리자는 미묘한 비대칭 속 조화를 보여주며, 라파엘로의 ‘아테네 학당’은 대칭과 원근법을 통해 아름다움의 질서를 구현한다. 건축물에서도 대칭과 비례는 중요한 요소였다. 샤르트르 대성당, 산피에트로 대성당, 산타 마리아 노벨라 성당 같은 작품들은 구조 전체가 수학적 비례와 대칭 속에서 설계되었고, 그 안에서 인간이 느끼는 시각적 안정감과 경외심을 이끌어냈다.수학자들은 숫자와 도형에서 아름다움을 발견했다. 그중에서도 가장 아름답다고 여긴 평면 도형은 정다각형이었다. 모든 변의 길이가 같고, 모든 내각의 크기가 동일한 정다각형은 균형과 대칭, 그리고 반복되는 질서를 담고 있다. 이런 구조적 완전함은 조화로움을 통해 수학적 아름다움의 본질을 보여준다. 원 안에 고르게 배치된 점들, 기하학적 구성의 출발점, 자연 속 대칭까지 — 정다각형은 단순함 속에서 가장 높은 조화를 보여주는 결정체였다.하지만 정다각형에서의 탐구는 한계가 있었다. 내각의 크기를 계산하거나, 변의 수를 늘려 어떤 형태로 수렴하는지를 살펴보는 정도였다. 예를 들어, 변이 무한히 많아지면 정다각형은 원에