생글생글

학습 길잡이 기타

파라볼라 안테나 단점, 쌍곡선으로 해결했죠

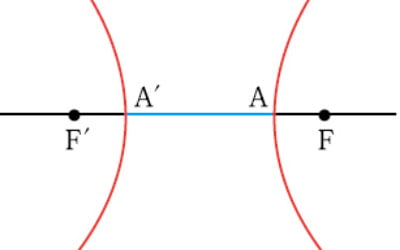
지난 생글생글 895호, 897호의 ‘재미있는 수학’에서는 이차곡선 중 타원, 포물선과 빛의 성질에 대해 살펴보았습니다. 이번에는 쌍곡선에 대해 알아보겠습니다.쌍곡선은 평면 위의 서로 다른 두 점 F, F′에서의 거리의 차가 일정한 점들의 집합이고, 두 점 F, F′을 쌍곡선의 ‘초점’이라고 합니다. 쌍곡선의 두 초점 F, F′을 잇는 직선이 쌍곡선과 만나는 두 점을 각각 A, A′이라고 할 때, 선분 AA′을 쌍곡선의 ‘주축’이라고 합니다.이러한 쌍곡선의 정의를 이용하면 항해 중인 배의 위치를 알아낼 수 있다고 합니다. 항해 중인 배의 위치를 찾을 때, 멀리 떨어져 있는 두 기지에서 동시에 전파를 보냅니다. 배는 보통 어느 한 기지에 더 가까이 있기 마련이므로, 두 기지에서 보낸 신호를 약간의 시차를 두고 받게 됩니다. 두 기지 A와 B에서 발신한 신호가 배에 도달하는 데 걸리는 시간을 각각 TA, TB 라 하고, 배의 위치를 P라 하면 다음 식이 성립합니다.(단, c는 전파의 속력)따라서 배는 두 점 A, B를 초점으로 하는 쌍곡선 위 어딘가에 있습니다. 배의 위치를 정확하게 알고 싶으면 서로 다른 세 지점으로부터 발신된 신호를 이용하면 됩니다. A 기지와 또 다른 한 기지인 C에서 전파를 보내 거리의 차를 구하면, 위와 마찬가지 방법으로 배가 위치하는 A와 C를 초점으로 하는 쌍곡선을 구할 수 있습니다. 그러면 A, B를 초점으로 하는 쌍곡선과 A, C를 초점으로 하는 쌍곡선의 교점을 구해 배의 정확한 위치를 파악할 수 있습니다.지난 생글생글 897호의 ‘재미있는 수학’에서 다룬, 포물선과 빛의 성질을 이용한 파라볼라 안테나는 포물면의 중심에서 초점까지 거리가 멀어지