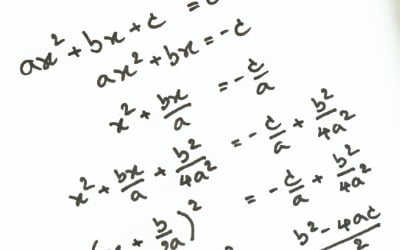생글생글

학습 길잡이 기타

'집합과 명제'는 논리적 사고력 키울 수 있어

어떤 사람이 논리적이라는 표현은 칭찬으로 이해되는 경우가 많지만 그렇지 않은 경우도 있습니다. 예를 들면, 성격 유형 검사인 MBTI와 관련해 다양한 오해와 선입견으로 ‘T’가 밈(meme)화 되고 있는 현상이 그렇습니다. 그럼에도 논리적 생각은 고차원의 사고 활동에서 필수적이고 중요한 수단이자 과정입니다.고교 교육과정에서는 논리학을 가르치지 않지만 학생들은 여러 과목을 통해 자연스럽게 논리적으로 무엇이 옳고 그른 것인지 알 수 있게 됩니다. 특히 수학은 모든 단원에서 추론(reasoning) 과정을 공부할 수 있는 과목입니다. 특히 ‘집합과 명제’ 단원은 이러한 논리적 사고방식을 수학적 기호를 활용해 연습할 수 있는 거의 유일한 단원입니다. 그래서 이 단원을 논리학의 기초적인 내용과 연계해 이해하면 유익합니다.논리적 추론을 크게 구분하면 연역적 추론과 귀납적 추론이 있습니다.예를 들어, [근거 1: 오늘 비가 오면 행사가 취소된다. 근거 2: 오늘 비 예보가 있다. 주장: 행사는 취소될 것이다.] 라는 논증을 봅시다. 이는 전형적인 연역적 추론으로서 형식적으로는 A이면 B이다, A이다, 그러므로 B이다. 라고 볼 수 있습니다. A와 B자리에 어떤 문장이 들어오더라도 근거로 쓰는 문장들이 참이라면 주장은 항상 참이 될 수 밖에 없습니다.다른 예를 들어봅시다. [근거 1: 어제 해가 떴다. 근거 2: 그제 해가 떴다. 근거 3: 1년 전에도 해가 떴다. 근거 4: 100년 전에도 해가 떴다. 주장: 그러므로 내일도, 앞으로도 계속 해가 뜰 것이다.] 이런 형태의 논증은 귀납추론이라고 합니다. 귀납추론의 근거들은 경험적으로, 사례 위주로 주장을 뒷받침합니다. 근거가 많을수록 강한 추론이 되며