생글생글

신철수 쌤의 국어 지문 읽기

모든 함수가 비례(반비례)하는 것이 아니라고?

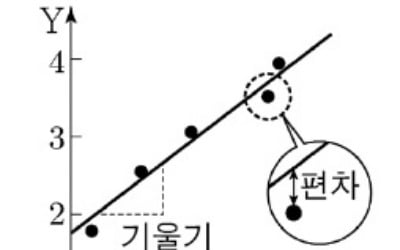
19세기의 초기 연구는 체외로 발산되는 열량이 체표 면적에 비례한다고 보았다. 즉 그 둘이 항상 일정한 비(比)를 갖는다는 것이다.(중략)1930년대에 클라이버는 생쥐부터 코끼리까지 다양한 크기의 동물의 기초 대사량 측정 결과를 분석했다. 그래프의 가로축 변수로 동물의 체중을, 세로축 변수로 기초 대사량을 두고, 각 동물별 체중과 기초 대사량의 순서쌍을 점으로 나타냈다.가로축과 세로축 두 변수의 증가율이 서로 다를 경우, 그 둘의 증가율이 같을 때와 달리, ‘일반적인 그래프’에서 이 점들은 직선이 아닌 어떤 곡선의 주변에 분포한다. 그런데 순서쌍의 값에 상용로그를 취해 새로운 순서쌍을 만들어서 이를 <그림>과 같이 그래프에 표시하면, 어떤 직선의 주변에 점들이 분포하는 것으로 나타난다. 그러면 그 직선의 기울기를 이용해 두 변수의 증가율을 비교할 수 있다. <그림>에서 X와 Y는 각각 체중과 기초 대사량에 상용로그를 취한 값이다. 이런 방식으로 표현한 그래프를 ‘L-그래프’라 하자.체중의 증가율에 비해, 기초 대사량의 증가율이 작다면 L-그래프에서 직선의 기울기는 1보다 작으며 기초 대사량의 증가율이 작을수록 기울기도 작아진다. 만약 체중의 증가율과 기초 대사량의 증가율이 같다면 L-그래프에서 직선의 기울기는 1이 된다. -2023학년도 대학수학능력시험- …이 …에 비례… 즉 그 둘이 항상 일정한 비(比)를 갖는다. … 가로축과 세로축 두 변수의 증가율이 서로 다를 경우, 그 둘의 증가율이 같을 때… 점들은 직선… 곡선의 주변에 분포‘A가 B에 비례한다’는 A가 종속 변수, B가 독립 변수인 함수 관계를 말한다고 했다.