생글생글

신철수 쌤의 국어 지문 읽기

그래프로 표현되는 함수!…그 또한 국어 능력이다

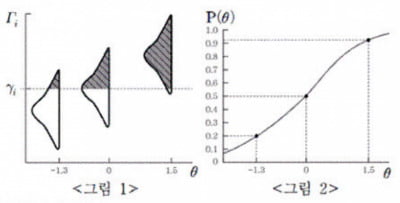
i라는 문항이 제시되었을 때 … i문항에 응답하는 경향(Γi)은 피험자의 능력(θ)에 따라 정규 분포로 그려지게 될 것이고, 문항의 난이도가 i일 때 Γi가 이보다 높으면 문항의 답을 맞히게 될 것이다. 즉 <그림1>과 같이 θ가 -1.3, 0, 1.5일 때 각각의 정규 분포가 그려진다면 i보다 위에 있는 면적이 문항의 답을 맞힐 확률이 되어, θ가 -1.3인 집단의 답을 맞힐 확률은 0.2, θ가 0인 집단의 답을 맞힐 확률은 0.5, θ가 1.5인 집단의 답을 맞힐 확률은 0.92로 얻어진다. 이런 방식으로 각 능력에서 문항의 답을 맞힐 확률인 P(θ)를 구하고, 이를 연결하는 곡선을 그리면 <그림2>와 같은 문항 특성 곡선이 나타난다.문항 특성 곡선은 능력이 낮은 집단의 P(θ)는 낮고, 능력이 높은 집단의 P(θ)는 높음을 나타내는 증가함수다. 문항 특성 곡선에서 문항의 난이도는 위치 모수로 나타난다. 위치 모수는 문항의 P(θ)가 0.5일 때 그에 대응하는 지점을 의미한다. 위치 모수는 오른쪽에 있을수록 어려운 문항으로 추정된다. 반면 문항의 변별도는 척도 모수로 나타난다. 척도 모수는 문항 특성 곡선의 기울기가 가파를수록 높다고 추정된다. (Γi)은 …(θ)에 따라 정규 분포로 그려지게 …일 때 …으면 …게 될 … 즉 <그림1>과 같이함수와 그것의 표현인 그래프는 수학적 사고로서, 국어 능력이라 했다. ‘A는 B에 따라 (그래프)로 그려지다’라는 문장은 함수를 나타낸다. 지문에서 ‘i문항에 응답하는 경향(Γi)은 피험자의 능력(θ)에 따라 정규 분포로 그려지’다고 했는데, 이는 ‘피험자의 능력(θ)’을 독립 변수, ‘i문